题目内容
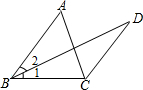
17．
如图，在△ABC中DE∥C，交AB，AC于点D，E，试证明$\frac{AD}{AB}=\frac{DO}{CO}$．
分析 由平行线的性质直接判断△ADE∽△ABC，△DOE∽△COB，写出比例式即可解决问题．
解答 证明：∵DE∥BC，
∴△ADE∽△ABC，△DOE∽△COB，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，$\frac{DO}{CO}=\frac{DE}{BC}$，
∴$\frac{AD}{AB}$=$\frac{DO}{CO}$．
点评 该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是熟练掌握相似三角形的判定和性质定理．
练习册系列答案
相关题目
7．已知扇形的弧长为20cm，面积为100cm2，则该扇形的半径为（ ）
| A． | 5πcm | B． | 5cm | C． | 10πcm | D． | 10cm |
5．点M（5，-6）先向右平移3个单位长度再向下平移2个单位长度的点的坐标是（ ）
| A． | （2，-8） | B． | （8，-8） | C． | （8，-4） | D． | （2，-4） |
12．下列二次根式最简二次根式是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{18}$ | C． | $\sqrt{56}$ | D． | $\sqrt{97}$ |
看图填空，并在括号内说明理由：
9．在Rt△ABC中，∠C=90°，若AC=4，AB=5，则cosB的值（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
在△ABC中，∠C=90°，△ABC的面积为6，斜边长为6，则tanA+tanB的值为3．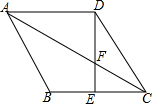
如图，菱形ABCD中，E为BC中点，DE与对角线AC交于点F，CF=DF．