题目内容

1．函数y=2x+5和y=$\frac{1}{2}$x-5的交点在第三象限．

分析 一次函y=2x+5的图象与一次函数y=$\frac{1}{2}$x-5联立方程组求解即可．

解答 解：$\left\{\begin{array}{l}{y=2x+5}\\{y=\frac{1}{2}x-5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-\frac{20}{3}}\\{y=-\frac{25}{3}}\end{array}\right.$，
所以函数y=2x+5和y=$\frac{1}{2}$x-5的交点在第三象限，
故答案为：第三．

点评 本题考查了两条直线相交的问题，属于基础题，关键是注意细心运算即可．

练习册系列答案
相关题目
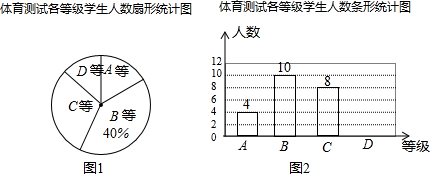
11．2011年成都市大约有3万名学生参加中考，为了考查他们的数学考试情况，评卷人抽取了1000名学生的数学成绩进行统计，那么下列四个判断正确的是（　　）
A．每名学生的数学成绩是个体B．3万名学生是总体
C．上述调查是普查D．1000名考生是总体的一个样本
12．在圆柱、正方体、长方体中，主视图可能一样的是（　　）
A．仅圆柱和正方体B．仅圆柱和长方体
C．仅正方体和长方体D．圆柱、正方体和长方体
9．本期开学以来，初2015级开展了轰轰烈烈的体育锻炼，为了解考体育科目训练的效果，九年级学生中随机抽取了部分学生进行了以此中考体育科目测试（把测试结果分为四个等级，A等：优秀；B等：良好；C等：及格；D等：不及格），并将结果汇成了如图1、2所示两幅不同统计图，请根据统计图中的信息解答下列问题：
（1）本次抽样测试的学生人数是25人；
（2）图1扇形图中D等所在的扇形的圆心角的度数是43.2°，并把图2条形统计图补充完整；
（3）我校九年级有1800名学生，如果全部参加这次中考体育科目测试，请估计不及格的人数为216人；
（4）已知得A等的同学有一位男生，体育老师想从4为同学中随机选择两位同学向其他同学介绍经验，请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率．
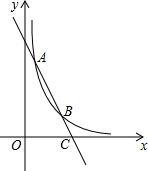16．如图，已知一次函数y=kx+b与反比例函数的图象交于点A（m，6）和B（2，3）．
（1）求反比例函数的解析式和求一次函数的解析式；
（2）根据图象回答，当x在什么范围内时，一次函数的值大于反比例函数的值？
（3）若直线y=kx+b与x轴交于点C，在x轴上是否存在点D，使得△BCD是以BC为腰的等腰三角形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
6．宁波、温州两地相距约300千米，一辆火车和一辆轿车先后从宁波出发去温州，设货车行驶的时间为x（小时），如图线段OA、折线BCD分别表示货车、轿车离宁波距离y（千米）与x（小时）之间的函数关系，根据图象解答下列问题：
（1）货车的行驶速度是60千米/时；轿车到达温州后，货车距离温州30千米．
（2）轿车在行驶过程中进行过一次变速，变速后过多长时间赶上货车？
13．如图，点A在x轴正半轴上，点B（4，m）在直线$y=\frac{1}{2}x$上，∠OBA=90°，BE∥x轴，交y轴于点E，C为OB中点，反比例函数$y=\frac{k}{x}$图象的一支经过点C，且与直线BE交于点D．
（1）k=2，直线AB的函数表达式为y=-2x+10；
（2）连结DC并延长，交x轴于点F，连结OD、BF，试判断四边形OFBD的形状并说明理由；
（3）M为直线AB上一点，若△BCM与△BOA相似，写出M点的坐标．
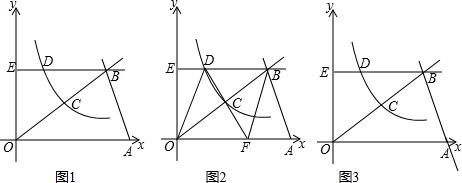
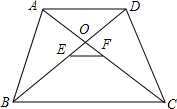10．如图：在四边形ABCD中，AD∥BC，AC、BD交于点O，E、F分别是AC、BD的中点，连接E、F，求证：EF∥BC，且EF=$\frac{1}{2}$（BC-AD）．
11．某商场计划购进A、B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
类型
价格		进价（元/盏）售价（元/盏）
A型3055
B型5070
（1）若商场预计进货款为3900元，则这两种台灯各购进多少盏？
（2）若商场规定A型台灯的进货数量不超过B型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网