题目内容
同一圆中的内接正六边形和内接正方形的周长比为 .
考点:正多边形和圆
专题:
分析:首先根据题意画出图形,设圆的半径为r,由正六边形的中心角等于60°,即可得△OAB为等边三角形,又由半径为r,即可求得正六边形的边长,进而得到周长;由正方形中心角为90°,可得NH=
,代入圆的半径为r,可得到NH的长,进而得到正方形周长,从而求得答案
| NO2+HO2 |
解答: 解:设圆的半径为r,
解:设圆的半径为r,
∵∠AOB=60°,AO=OB=r,
∴AB=r,
∴正六边形的周长为:6r,
∵∠NOH=90°,NO=OH=r,
∴NH=
=
r,
∴正方形周长是:4
r,
∴正六边形和正方形的周长比为:6r:4
r=3
:4,
故答案为:3
:4.
 解:设圆的半径为r,
解:设圆的半径为r,∵∠AOB=60°,AO=OB=r,
∴AB=r,
∴正六边形的周长为:6r,
∵∠NOH=90°,NO=OH=r,
∴NH=
| NO2+HO2 |
| 2 |
∴正方形周长是:4
| 2 |
∴正六边形和正方形的周长比为:6r:4
| 2 |
| 2 |
故答案为:3
| 2 |
点评:本题考查的是正多边形和圆,根据题意画出图形,再分别求出正六边形和正方形的边长是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
下列说法错误的是( )


| A、图①中直线l经过点A |
| B、图②中直线a,b相交于点A |
| C、图③中点C在线段AB上 |
| D、图④中射线CD与AB有公共点 |
 如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是
如图所示,点B,C是线段AD上任意两点,点M是AB的中点,点N是CD的中点.若AD=27,BC=5,则线段MN的长是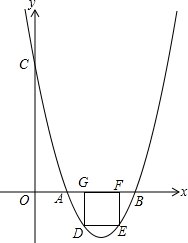 如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.
如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.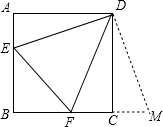 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. 如图,已知四个点A、B、C、D,根据下列要求画图:
如图,已知四个点A、B、C、D,根据下列要求画图: 已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为
已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm,则线段AB的长为