题目内容
17. 已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )
已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )| A. | 2b | B. | -2a | C. | -2b | D. | 2a |
分析 根据数轴可以判断a、b的大小和正负,由|a|>|b|,从而可以化简$\sqrt{(a+b)^{2}}$-|a-b|,本题得以解决.
解答 解:由数轴可得,a<0<b,
∵|a|>|b|,
∴a+b<0,a-b<0,
∴$\sqrt{(a+b)^{2}}$-|a-b|
=-(a+b)+(a-b)
=-a-b+a-b
=-2b,
故选C.
点评 本题考查实数与数轴,解题的关键是明确数轴的特点,能对二次根式进行化简.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
5.小李将1000元钱存入银行,年利率为x,第二年他把本息和全部存入银行,两年后不计利息税,他得到本息共a元,则依题意可列方程为( )
| A. | 1000(x+x)=a | B. | 1000(1-2x)=a | C. | 1000(1+x)2=a | D. | 1000(1+2x)2=a |
2.下列语句是命题的是( )
| A. | 相等的角是对顶角 | B. | 同位角相等,两直线平行吗? | ||
| C. | 作∠AOB的平分线OC | D. | 延长线AB到C使AC=2AB |
6.已知△ABC的三个内角∠A,∠B,∠C满足∠A=∠B=∠C,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 钝角三角形 |
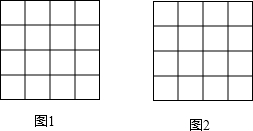 如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.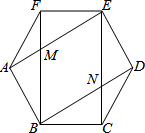 如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.