题目内容
3．已知函数y=（m-2）x${\;}^{{m}^{2}-2}$+4x+7是二次函数，则m的值为（ ）| A． | -2 | B． | ±2 | C． | $\sqrt{3}$ | D． | ±$\sqrt{3}$ |
分析 直接利用二次函数的定义得出关于m的等式进而得出答案．
解答 解：∵函数y=（m-2）x${\;}^{{m}^{2}-2}$+4x+7是二次函数，
∴m2-2=2，且m-2≠0，
解得：m=-2．
故选：A．
点评 此题主要考查了二次函数的定义，正确把握二次函数的定义是解题关键．
练习册系列答案
相关题目
13．
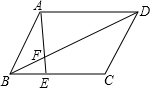如图，点E是平行四边形ABCD边BC上一点，BE：EC=4：1，AE交BD于F点，BF：FD等于（ ）
如图，点E是平行四边形ABCD边BC上一点，BE：EC=4：1，AE交BD于F点，BF：FD等于（ ）| A． | 4：5 | B． | 4：9 | C． | 5：9 | D． | 4：10 |
11．下列说法正确的是（ ）
| A． | 延长射线得直线 | B． | 过两点有且只有一条直线 | ||
| C． | 直线就是一个平角 | D． | 过三点一定能作三条直线 |
18．
如图，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，且∠DOE=60°，∠BOE=$\frac{1}{3}$∠EOC，则下列四个结论正确的个数有（ ）
①∠BOD=30°；②射线OE平分∠AOC；③图中与∠BOE互余的角有2个；④图中互补的角有6对．
如图，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，且∠DOE=60°，∠BOE=$\frac{1}{3}$∠EOC，则下列四个结论正确的个数有（ ）①∠BOD=30°；②射线OE平分∠AOC；③图中与∠BOE互余的角有2个；④图中互补的角有6对．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．在质地和颜色都相同的三张卡片的正面分别写有-2，-1，1，将三张卡片背面朝上洗匀，从中抽出一张，并记为x，然后从余下的两张中再抽出一张，记为y，则点（x，y）在反比例函数y=$\frac{2}{x}$图象上的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | 1 |
15．下列关于几何画图的语句正确的是（ ）
| A． | 延长射线AB到点C，使BC=2AB | |
| B． | 点P在线段AB上，点Q在直线AB的反向延长线上 | |
| C． | 将射线OA绕端点O旋转180°，终边OB与始边OA形成一个平角 | |
| D． | 连接BC，使BC=2cm |
12．
如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）
如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠D=∠DCE | D． | ∠D+∠ACD=180° |
13．计算（3x-1）（1-3x）结果正确的是（ ）
| A． | 9x2-1 | B． | 1-9x2 | C． | -9x2+6x-1 | D． | 9x2-6x+1 |