题目内容
17.下列命题中,真命题是( )| A. | 两个无理数相加的和一定是无理数 | B. | 三角形的三条中线一定交于一点 | ||
| C. | 菱形的对角线一定相等 | D. | 同圆中相等的弦所对的弧一定相等 |
分析 根据菱形的性质、无理数的性质、三角形中线的性质以及同圆中相等的弦所对的弧不一定相等即可判断.
解答 解:A、错误.例如1+$\sqrt{2}$与1-$\sqrt{2}$都是无理数,它们的和是有理数.
B、正确.
C、错误.菱形的对角线不一定相等.
D、错误.应该是同圆中相等的弦所对的劣弧或优弧相等.
故选B.
点评 本题考查命题与定理、无理数的性质、三角形中线的性质、菱形的性质、圆的有关知识,解题的关键是正确理解概念,记住这些基本性质,属于中考常考题型.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
7.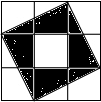 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
8.小明从一副扑克牌中取出3张红桃、2张黑桃共5张牌与弟弟做游戏,把这5张牌背面朝上洗匀后放在桌子上,小明与弟弟同时各抽一张,两人抽到花色相同的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
5.下列各式结果正确的是( )
| A. | 20=0 | B. | 3-1=-3 | C. | $\sqrt{9}$=±3 | D. | tan60°=$\sqrt{3}$ |
2.-3×(-2)=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | $-\frac{1}{6}$ |
6.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
7.不等式2x+4≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是10.
如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是10.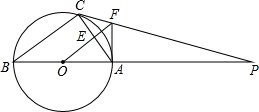 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.