题目内容
15.正数m,n满足m+4$\sqrt{mn}-2\sqrt{m}-4\sqrt{n}$+4n=3,则$\frac{{\sqrt{m}+2\sqrt{n}-8}}{{\sqrt{m}+2\sqrt{n}+2006}}$的值为-$\frac{5}{2009}$.分析 首先把m+4$\sqrt{mn}-2\sqrt{m}-4\sqrt{n}$+4n=3在实数范围内利用因式分解求得$\sqrt{m}$+2$\sqrt{n}$,再进一步代入求得答案即可.
解答 解:∵m+4$\sqrt{mn}-2\sqrt{m}-4\sqrt{n}$+4n=3,
∴m+4$\sqrt{mn}$+4n-2($\sqrt{m}$+2$\sqrt{n}$)-3=0,
∴($\sqrt{m}$+2$\sqrt{n}$)2-2($\sqrt{m}$+2$\sqrt{n}$)-3=0,
∴($\sqrt{m}$+2$\sqrt{n}$-3)($\sqrt{m}$+2$\sqrt{n}$+1)=0,
∴$\sqrt{m}$+2$\sqrt{n}$=3,$\sqrt{m}$+2$\sqrt{n}$)=-1(不合题意,舍去)
∴$\frac{{\sqrt{m}+2\sqrt{n}-8}}{{\sqrt{m}+2\sqrt{n}+2006}}$=$\frac{3-8}{3+2006}$=-$\frac{5}{2009}$.
故答案为:-$\frac{5}{2009}$.
点评 此题考查二次根式的化简求值,利用因式分解求得$\sqrt{m}$+2$\sqrt{n}$的值是解决问题的关键,渗透整体代入的思想.

练习册系列答案
相关题目
3.把26个英文大写字母看成图案:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z,则成中心对称图案的字母共有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
4.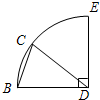 如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )
如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )
 如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )
如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )| A. | 0°≤∠C≤45° | B. | 0°<∠C≤45° | C. | 45°<∠C<90° | D. | 45°≤∠C<90° |
 如图所示,AB=DC,AD=BC,直线EF交DC的延长线于E,交AB于F,求证:∠E=∠BFE.
如图所示,AB=DC,AD=BC,直线EF交DC的延长线于E,交AB于F,求证:∠E=∠BFE. 如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=2:3,AC=15,求DE的长.
如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=2:3,AC=15,求DE的长.