Question

4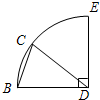．如图，弧BE是⊙D的$\frac{1}{4}$圆周，点C在弧BE上运动（不与B重合），则∠C的取值范围是（　　）

• A． 0°≤∠C≤45°
• B． 0°＜∠C≤45°
• C． 45°＜∠C＜90°
• D． 45°≤∠C＜90°

Answer 1

分析 由于$\widehat{BE}$是⊙D的$\frac{1}{4}$圆周，则可计算出∠BDE=90°，再根据等腰三角形的性质由DB=DC，则∠B=∠BCD，于是根据三角形内角和定理得到∠BCD=90°-$\frac{1}{2}$∠BDC，然后根据0≤∠BDC≤90°求∠BCD的取值范围．

解答 解：∵$\widehat{BE}$是⊙D的$\frac{1}{4}$圆周，
∴∠BDE=$\frac{1}{4}$×360°=90°，
∵DB=DC，
∴∠B=∠C，
∴∠C=$\frac{1}{2}$（180°-∠BDC）=90°-$\frac{1}{2}$∠BDC，
∵0≤∠BDC≤90°，
∴45°≤∠C≤90°，
故选D．

点评 本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了等腰三角形的性质．