题目内容
7.在△ABC和△DEF中,已知$\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$=$\frac{3}{4}$,且△ABC的周长为18cm,求△DEF的周长.分析 根据三边对应成比例两三角形相似得到△ABC∽△DEF,然后由三角形的相似比等于三角形的周长比,即可求得结论.
解答 解:∵$\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$=$\frac{3}{4}$,
∴△ABC∽△DEF,
∴△ABC的周长:△DEF的周长=$\frac{AB}{DE}$=$\frac{3}{4}$,
∵△ABC的周长为18cm,
∴△DEF的周长=24cm.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.如果“赚了100元”记为+100,那么“亏损200元”记为( )
| A. | +200 | B. | -100 | C. | -200 | D. | -300 |
2. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2,
其中说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2,
其中说法正确的是( )
| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
12.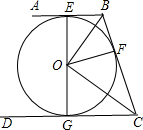 如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )
如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )
 如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )
如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
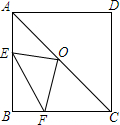 如图,边长为4cm的正方形ABCD,对角线AC,BD相交于点O,E是AB边上一动点(与A.B不重合),过点O作OF⊥OE交BC边于F.
如图,边长为4cm的正方形ABCD,对角线AC,BD相交于点O,E是AB边上一动点(与A.B不重合),过点O作OF⊥OE交BC边于F.