题目内容
12.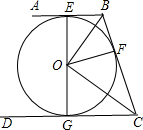 如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )
如图,AB,BC,CD分别切⊙O于点E、F、G,且AB∥CD,BO=3cm,CO=4cm,则BC等于( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
分析 根据切线长定理可得∠EBO=∠FBO,∠GCO=∠FCO,根据平行线的性质可得∠EBC+∠GCB=180°,由此可得∠FBO+∠FCO=90°,则有∠BOC=90°,然后运用勾股定理即可求出BC.
解答 解:∵AB,BC,CD分别切⊙O于点E、F、G,
∴∠EBO=∠FBO,∠GCO=∠FCO.
∵AB∥CD,
∴∠EBC+∠GCB=180°,
∴2∠FBO+2∠FCO=180°,
∴∠FBO+∠FCO=90°,
∴∠BOC=90°.
∵BO=3cm,CO=4cm,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5(cm).
故选A.
点评 本题主要考查了切线长定理、平行线的性质、勾股定理等知识,证到∠BOC=90°是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.有个花园占地面积约为 800000平方米,若按比例尺1:2000缩小后,其面积大约相当于( )
| A. | 一个篮球场的面积 | B. | 一张乒乓球台台面的面积 | ||
| C. | 《钱江晚报》一个版面的面积 | D. | 《数学》课本封面的面积 |
2.小刚想利用下列长度的木棒摆成一个三角形,下列各组你认为可行的是( )
| A. | 5,2,2 | B. | 2,3,6 | C. | 2,3,4 | D. | 7,13,6 |
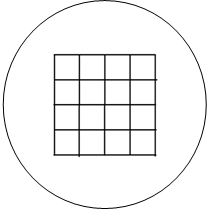 一座圆形花坛的半径为r,中间喷水池是面积为4的正方形.
一座圆形花坛的半径为r,中间喷水池是面积为4的正方形.