题目内容
6.曾都区某中学九年级去随县尚市镇牡丹基地参加社会实践活动,该基地有桃树和牡丹两种经济作物.已知该基地有甲乙两家种植户,种植面积与销售总收入如下表.(假设不同种植户种植的同种作物每亩平均收入相等)| 种植户 | 桃树种植面积(亩) | 牡丹种植面积(亩) | 销售总收入(元) |
| 甲 | 5 | 3 | 33500 |
| 乙 | 3 | 7 | 43500 |
(2)甲、乙种植户计划合租30亩地用来种植桃树和牡丹,根据市场调查,要求桃树的种植面积大于牡丹的种植面积(两种作物的种植面积均为整数亩),基地对种植桃树给予补贴,种植桃树的面积不超过15亩的部分,每亩补贴100元;超过15亩但不超过20亩的部分,每亩补贴200元;超过20亩的部分每亩补贴300元.为了使总收入不低于127500元,则他们有几种种植方案?
分析 (1)设桃树每亩平均收入为x元,牡丹每亩平均收入为y元,根据表格中的等量关系列出方程组求解;
(2)设种植桃树m亩,则种植牡丹面积为(30-m)亩,根据桃树的种植面积大于牡丹的种植面积,可得m>15,然后分段讨论求解.
解答 解:(1)设桃树每亩平均收入为x元,牡丹每亩平均收入为y元,
依题意得:$\left\{\begin{array}{l}{5x+3y=33500}\\{3x+7y=43500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4000}\\{y=4500}\end{array}\right.$.
答:桃树每亩的收入为4000元,牡丹每亩的平均收入是4500元.
(2)设种植桃树m亩,则种植牡丹面积为(30-m)亩,
依题意得:m>30-m,
解得:m>15,
当15<m≤20时,总收入w=4000m+4500(30-m)+15×100+(m-15)×200≥127500,
解得:15<m≤20,
当m>20时,总收入w=4000m+4500(30-m)+15×100+5×200+(m-20)×300≥127500,
解得:m≤20,(不合题意),
综上所述,种植方案如下:
| 种植类型 | 种植面积(亩) | ||||
| 方案一 | 方案二 | 方案三 | 方案四 | 方案五 | |
| 桃树 | 16 | 17 | 18 | 19 | 20 |
| 牡丹 | 14 | 13 | 12 | 11 | 10 |
点评 本题考查了二元一次方程组的应用及一元一次不等式的应用,解答本题的关键是仔细审题,找到等量关系与不等关系.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.某技工培训中心有钳工20名、车工30名.现将这50名技工中的15人派往A地工作,35人派往B地工作,两地技工的工资情况如下表:
设派往A地x名钳工时,这50名技工的月工资总额为y元.
(1)派往B地20-x名钳工,派往B地15+x名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
| 工种 属地 | 钳工 | 车工 |
| A地 | 1800(元/月) | 1600(元/月) |
| B地 | 1600(元/月) | 1200(元/月) |
(1)派往B地20-x名钳工,派往B地15+x名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
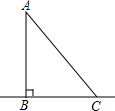 某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.
某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.