题目内容
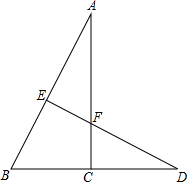 如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.
如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.考点:全等三角形的判定与性质
专题:
分析:根据全等三角形的判定与性质,可得BC=BE,∠A=∠D,根据AAS,可得△AEF≌△DCF,根据全等三角形的性质,可得AF与DF的关系,根据等量代换,可得答案.
解答:解:在△ABC和△DBE中,
,
∴△ABC≌△DBE(SAS),
∴BC=BE,∠A=∠D.
∵AB-BE=BD-BC,
∴AE=CD.
在△AEF和△DCF中,
,
∴△AEF≌△DCF(AAS),
∴AF=DF.
∵CF+AF=AE,
∴CF+DF=AE=2.5(cm).
|
∴△ABC≌△DBE(SAS),
∴BC=BE,∠A=∠D.
∵AB-BE=BD-BC,
∴AE=CD.
在△AEF和△DCF中,
|
∴△AEF≌△DCF(AAS),
∴AF=DF.
∵CF+AF=AE,
∴CF+DF=AE=2.5(cm).
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
正方形具有而菱形不具有的性质是( )
| A、对角线平分一组对角 |
| B、对角线相等 |
| C、对角线互相垂直平分 |
| D、四条边相等 |
下列判断中正确的是( )
| A、全等三角形是面积相等的三角形 |
| B、面积相等的三角形都是全等的三角形 |
| C、等边三角形都是面积相等的三角形 |
| D、面积相等斜边相等的直角三角形都是全等直角三角形 |
 如图,已知AF=BE,∠A=∠B,AC=BD,经分析
如图,已知AF=BE,∠A=∠B,AC=BD,经分析 如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是
如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是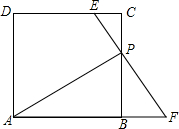 如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.
如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.