题目内容
 如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是
如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是考点:正方形的性质
专题:
分析:根据正方形的性质可以证明△AEO≌CFO,就可以得出S△AEO=S△CFO,就可以求出△AOD面积等于正方形面积的
,根据正方形的面积就可以求出结论.
| 1 |
| 4 |
解答:解:∵四边形ABCD是正方形,
∴AO=CO,∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AEO≌CFO(ASA),
∴S△AEO=S△CFO,
∴S△AOD=S△DEO+S△CFO,
∵S正方形ABCD=52=25,
∴S△AOD=
,
∴阴影部分的面积为
.
故答案为:
.
∴AO=CO,∠EAO=∠FCO,
在△AOE和△COF中,
|
∴△AEO≌CFO(ASA),
∴S△AEO=S△CFO,
∴S△AOD=S△DEO+S△CFO,
∵S正方形ABCD=52=25,
∴S△AOD=
| 25 |
| 4 |
∴阴影部分的面积为
| 25 |
| 4 |
故答案为:
| 25 |
| 4 |
点评:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,正方形的面积及三角形的面积公式的运用,在解答时证明△AEO≌CFO是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则
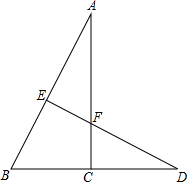 如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.
如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.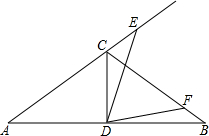 如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上
如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上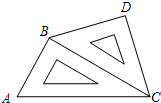 如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.
如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.