题目内容
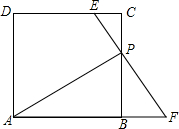 如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.
如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.(1)当点P在线段CB上时(如图1),求证:BP=EC+BE;
(2)当点P在CB的延长线上时,画出图形,猜想线段BP、EC、BF之间的数量关系并加以证明.
考点:正方形的性质,相似三角形的判定与性质
专题:
分析:(1)先根据正方形的性质求得PC+PB=BC=AB,然后证得△PFB∽△PEC,得出PC•BF=PB•CE,在直角三角形PAF中,PB是斜边AF上的高,根据射影定理得出
PB2=AB•BF=BC•BF=(PB+PC)•BF=PB•BF+PC•BF=PB•BF+PB•CE=PB•(BF+CE),即可证得结论;
(2))先根据正方形的性质求得PC-PB=BC=AB,然后证得△PFB∽△PEC,得出PC•BF=PB•CE,在直角三角形PAF中,PB是斜边AF上的高,根据射影定理得出PB2=AB•BF=BC•BF=(PC-PB)•BF=PC•BF-PB•BF=PB•CE-PB•BF=PB•(CE-BF),即可证得结论;
PB2=AB•BF=BC•BF=(PB+PC)•BF=PB•BF+PC•BF=PB•BF+PB•CE=PB•(BF+CE),即可证得结论;
(2))先根据正方形的性质求得PC-PB=BC=AB,然后证得△PFB∽△PEC,得出PC•BF=PB•CE,在直角三角形PAF中,PB是斜边AF上的高,根据射影定理得出PB2=AB•BF=BC•BF=(PC-PB)•BF=PC•BF-PB•BF=PB•CE-PB•BF=PB•(CE-BF),即可证得结论;
解答: (1)证明:如图1,∵ABCD为正方形
(1)证明:如图1,∵ABCD为正方形
∴PC+PB=BC=AB
∵AP⊥EF,CB⊥AB
∵在直角三角形PCE和直角三角形PBF中,∠BPF=∠CPE
∴△PFB∽△PEC
∴
=
,
∴PC•BF=PB•CE
∵PA⊥EF,PB⊥AB
∴在直角三角形PAF中,PB是斜边AF上的高
∴PB2=AB•BF=BC•BF=(PB+PC)•BF=PB•BF+PC•BF=PB•BF+PB•CE=PB•(BF+CE)
∴BP=EC+BF.
(2)BP=EC-BF.
证明:如图2,
∵四边形ABCD为正方形
∴PC-PB=BC=AB
∵AP⊥EF,CB⊥AB
∵在直角三角形PCE和直角三角形PBF中,∠BPF=∠CPE
∴△PFB∽△PEC
∴
=
,
∴PC•BF=PB•CE
∵PA⊥EF,PB⊥AB
∴在直角三角形PAF中,PB是斜边AF上的高
∴PB2=AB•BF=BC•BF=(PC-PB)•BF=PC•BF-PB•BF=PB•CE-PB•BF=PB•(CE-BF)
∴BP=EC-BF.
 (1)证明:如图1,∵ABCD为正方形
(1)证明:如图1,∵ABCD为正方形∴PC+PB=BC=AB
∵AP⊥EF,CB⊥AB
∵在直角三角形PCE和直角三角形PBF中,∠BPF=∠CPE
∴△PFB∽△PEC
∴
| PB |
| PC |
| BF |
| CE |
∴PC•BF=PB•CE
∵PA⊥EF,PB⊥AB
∴在直角三角形PAF中,PB是斜边AF上的高
∴PB2=AB•BF=BC•BF=(PB+PC)•BF=PB•BF+PC•BF=PB•BF+PB•CE=PB•(BF+CE)
∴BP=EC+BF.
(2)BP=EC-BF.
证明:如图2,
∵四边形ABCD为正方形
∴PC-PB=BC=AB
∵AP⊥EF,CB⊥AB
∵在直角三角形PCE和直角三角形PBF中,∠BPF=∠CPE
∴△PFB∽△PEC
∴
| PB |
| PC |
| BF |
| CE |
∴PC•BF=PB•CE
∵PA⊥EF,PB⊥AB
∴在直角三角形PAF中,PB是斜边AF上的高
∴PB2=AB•BF=BC•BF=(PC-PB)•BF=PC•BF-PB•BF=PB•CE-PB•BF=PB•(CE-BF)
∴BP=EC-BF.
点评:本题考查了正方形的性质,相似三角形的判定和性质,射影定理的应用,熟练掌握性质定理是关键.

练习册系列答案
相关题目
下列图形是棱锥的是( )
A、 |
B、 |
C、 |
D、 |

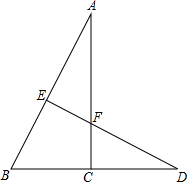 如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.
如图,已知在△ABC中,BC⊥AC,在BC的延长线上取一点D,使BD=BA,在AB边上取一点E,使BE=BC,连接DE并交AC于点F,若AC=2.5cm,求CF+DF的长.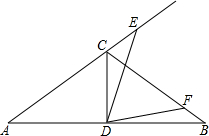 如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上
如图,在△ABC中,AC=BC,∠A=30°,D为AB的中点,∠EDF=60°,E,F分别在AC,BC上