题目内容
1.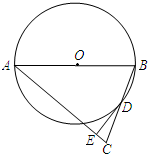 如图,已知△ABC中,AB=AC,以AB为直径的⊙O与BC边相交于点D,⊙O的切线DE交AC于点E.
如图,已知△ABC中,AB=AC,以AB为直径的⊙O与BC边相交于点D,⊙O的切线DE交AC于点E.(1)求证:BD=DC;
(2)判断DE与AC的位置关系,并说明理由;
(3)若⊙O的直径为32,cos∠B=$\frac{1}{4}$,求CE的长.
分析 (1)由AB为⊙O直径得到∠ADC=90°,而AC=AB,得到结论;
(2)先判断出∠CAD=∠ODA,再判断出∠CAD+∠ADE=90°即可;
(3)先由cos∠B=$\frac{1}{4}$,得出BD=8,再判断出△DEC∽△ADC,得到$\frac{EC}{DC}=\frac{DC}{AC}$,代值计算即可.
解答 解:(1)如图:连接AD,∵AB为⊙O的直径,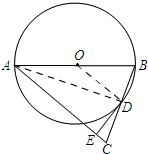 ∴∠ADB=90°,
∴∠ADB=90°,
∵AB=AC,
∴∠BAD=∠CAD,DB=DC,
即:DB=DC,
(2)DE⊥AC,连接OD,
由(1)∠BAD=∠CAD
∵OA=OD,
∴∠BAD=∠ODA,
∴∠CAD=∠ODA,
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ODA+∠ADE=90°,
∴∠CAD+∠ADE=90°,
∴∠AED=90°,
∴DE⊥AC;
(3∵⊙O的直径为32,cos∠B=$\frac{1}{4}$,
∴cos∠B=$\frac{BD}{AB}$=$\frac{BD}{32}$=$\frac{1}{4}$,
∴BD=8,
∴CD=BD=8,
∵∠C=∠C,∠DEC=∠ADC=90°,
∴△DEC∽△ADC,
∴$\frac{EC}{DC}=\frac{DC}{AC}$,
∵AC=AB=32,
∴$\frac{EC}{8}=\frac{8}{32}$,
∴EC=2.
点评 此题是圆的综合题,主要考查了直径所对对的圆周角为直角,切线的性质,锐角三角函数,三角形相似的判定和性质,直角三角形的判定,解本题的关键灵活运用互余判断出角相等或互余.

练习册系列答案
相关题目
9.如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )


| A. | 线段BE | B. | 线段EF | C. | 线段CE | D. | 线段DE |
16.如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )
| A. | S和C | B. | S和a | C. | C和a | D. | S,C,a |
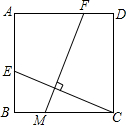 已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM.
已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM. 已知:反比例函数y1=$\frac{k}{x}$(k≠0,x>0)与一次函数y2=ax+b的图象相交于点A(1,8),B(4,m)两点.
已知:反比例函数y1=$\frac{k}{x}$(k≠0,x>0)与一次函数y2=ax+b的图象相交于点A(1,8),B(4,m)两点. 四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.
四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.