题目内容
19.计算:(1)$\frac{{\sqrt{20}+\sqrt{5}}}{{\sqrt{5}}}-2$
(2)$\sqrt{32}$-$\sqrt{\frac{1}{2}}$-$\sqrt{18}$
(3)4×($\sqrt{3}$+$\sqrt{7}$)0+$\sqrt{\frac{1}{2}}$×$\sqrt{8}$-(1-$\sqrt{2}$)2
(4)解方程组:$\left\{\begin{array}{l}3m-2n=-8\\ m+4n=2\end{array}\right.$.
分析 (1)首先化简二次根式,然后计算除法,最后加减即可;
(2)首先对二次根式进行化简,然后合并同类二次根式即可;
(3)首先计算0次幂,二次根式的乘法,利用完全平方公式计算二次根式的平方,最后合并同类二次根式即可;
(4)利用加减法即可求解.
解答 解:(1)原式=$\frac{2\sqrt{5}+\sqrt{5}}{\sqrt{5}}$-2=3-2=1;
(2)原式=4$\sqrt{2}$-$\frac{\sqrt{2}}{2}$-3$\sqrt{2}$=$\frac{\sqrt{2}}{2}$;
(3)原式=4×1+$\sqrt{4}$-(3-2$\sqrt{2}$)=4+2-3+2$\sqrt{2}$=3+2$\sqrt{2}$;
(4)$\left\{\begin{array}{l}{3m-2n=-8…①}\\{m+4n=2…②}\end{array}\right.$,
①×2+②得7m=-14,
解得m=-2,
把m=-2代入②得-2+4n=2,
解得n=1.
则方程组的解是:$\left\{\begin{array}{l}m=-2\\ n=1\end{array}\right.$.
点评 本题考查了方程组的解法以及二次根式的混合运算,二次根式乘法、除法及加减法运算法则的综合运用中与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
14.A、B两地相距135千米,两辆汽车均从A开往B,大汽车比小汽车早出发5小时,小汽车比大汽车早到30分钟,已知小汽车与大汽车的速度之比为5:2,若小汽车的速度为5x千米/小时,则可列方程为( )
| A. | $\frac{135}{2x}$=$\frac{135}{5x}$+5+$\frac{1}{2}$ | B. | $\frac{135}{2x}$=$\frac{135}{5x}$+5-$\frac{1}{2}$ | ||
| C. | $\frac{135}{5x}$=$\frac{135}{2x}$+5-$\frac{1}{2}$ | D. | $\frac{135}{5x}$=$\frac{135}{2x}$-5-$\frac{1}{2}$ |
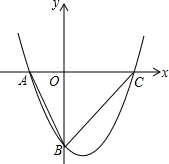 如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.
如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.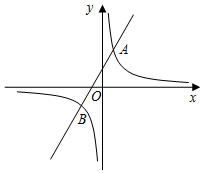 已知反比例函数${y_1}=\frac{k}{x}$的图象与一次函数y2=2x+b 的图象交于点A(1,4)和点B(m,-2).
已知反比例函数${y_1}=\frac{k}{x}$的图象与一次函数y2=2x+b 的图象交于点A(1,4)和点B(m,-2).