题目内容
19.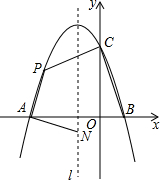 如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1.(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
分析 (1)将已知点的坐标代入已知的抛物线的解析式,利用待定系数法确定抛物线的解析式即可;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PE=OA,从而得到方程求得x的值即可求得点P的坐标;
②用分割法将四边形的面积S四边形BCPA=S△OBC+S△OAC,得到二次函数,求得最值即可.
解答 解:(1)∵抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=-1,
∴$\left\{\begin{array}{l}{a+b+c=0}\\{c=3}\\{-\frac{b}{2a}=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$.
∴二次函数的解析式为y=-x2-2x+3=-(x+1)2+4,
∴顶点坐标为(-1,4);
(2)令y=-x2-2x+3=0,解得x=-3或x=1,
∴点A(-3,0),B(1,0),
作PD⊥x轴于点D,
∵点P在y=-x2-2x+3上,
∴设点P(x,-x2-2x+3)
①∵PA⊥NA,且PA=NA,
∴△PAD≌△ANQ,
∴AQ=PD,
即y=-x2-2x+3=2,
解得x=$\sqrt{2}$-1(舍去)或x=-$\sqrt{2}$-1,
∴点P(-$\sqrt{2}$-1,2);
②设P(x,y),则y=-x2-2x+3,
由于P在第二象限,所以其横坐标满足:-3<x<0,
∵S四边形PABC=S△OBC+S△APO+S△OPC,
S△OBC=$\frac{1}{2}$OB•OC=$\frac{1}{2}$×3×1=$\frac{3}{2}$,
S△APO=$\frac{1}{2}$AO•|y|=$\frac{1}{2}$×3•y=$\frac{3}{2}$y=$\frac{3}{2}$(-x2-2x+3)=-$\frac{3}{2}$x2-3x+$\frac{9}{2}$,
S△OPC=$\frac{1}{2}$CO•|x|=$\frac{1}{2}$×3•(-x)=-$\frac{3}{2}$x,
∴S四边形PABC=$\frac{3}{2}$-$\frac{3}{2}$x2-3x+$\frac{9}{2}$-$\frac{3}{2}$x=6-$\frac{9}{2}$x-$\frac{3}{2}$x2=-$\frac{3}{2}$(x+$\frac{3}{2}$)2+$\frac{75}{8}$,
∴当x=-$\frac{3}{2}$时,S四边形PABC最大值=$\frac{75}{8}$,此时y=-x2-2x+3=$\frac{15}{4}$,
所以P(-$\frac{3}{2}$,$\frac{15}{4}$).
点评 本题考查了二次函数综合题.用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法.求抛物线的最值的方法是配方法.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | ±2 | B. | 16 | C. | -2 | D. | 2 |
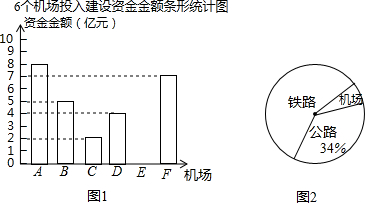
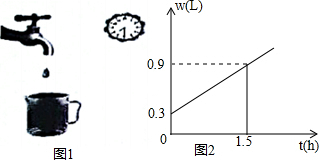
(1)机场建设项目中所有6个机场投入的建设资金金额统计如图1,已知机场E投入的建设资金金额是机场C,D所投入建设资金金额之和的三分之二,求机场E投入的建设资金金额是多少亿元?并补全条形统计图;
(2)将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表,根据扇形统计图及统计表中信息,求得a=170,b=30,c60%,d122.4°,m=500.(请直接填写计算结果)
| 铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
| 投入资金(亿元) | 300 | a | b | m |
| 所占百分比 | c | 34% | 6% | |
| 所占圆心角 | 216° | d | 21.6° |
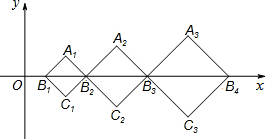 如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.
如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.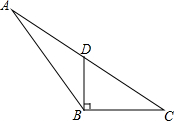 如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5. 如图,是由四个完全相同的小正方形组成的立体图形,它的俯视图是( )
如图,是由四个完全相同的小正方形组成的立体图形,它的俯视图是( )



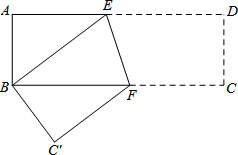 如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )