题目内容
3. 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=0H.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=0H.
分析 由菱形的性质得出AB=BC=CD=DA,OB=OD,OA=OC,证出OE是△ABD的中位线,由三角形中位线定理得出OE=$\frac{1}{2}$DA,同理:OF=$\frac{1}{2}$CD,OG=$\frac{1}{2}$BC,OH=$\frac{1}{2}$AB,即可得出结论.
解答 证明:如图所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OB=OD,OA=OC,
∵E是AB的中点,
∴OE是△ABD的中位线,
∴OE=$\frac{1}{2}$DA,
同理:OF=$\frac{1}{2}$CD,OG=$\frac{1}{2}$BC,OH=$\frac{1}{2}$AB,
∴OE=OF=OG=0H.
点评 本题考查了菱形的性质、三角形中位线定理;熟练掌握菱形的性质,由三角形中位线定理得出OE=$\frac{1}{2}$DA是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.下列各图,是轴对称图形的有( )个.


| A. | 2 | B. | 3 | C. | 4 | D. | 4 |
12.一袋中有10个红球,4个黄球,每个球除颜色外都相同,从袋中任意摸出一个而得到是红球的可能性是( )
| A. | $\frac{5}{7}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{14}$ |
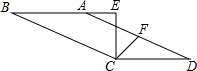 如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.
如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.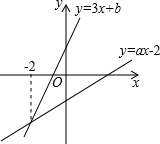 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.