题目内容

已知函数y=
k
x
的图象经过点（2，3），那么图象应在（　　）
A、第一、三象限
B、第一、二象限
C、第二、四象限
D、第三、四象限
考点：反比例函数图象上点的坐标特征
专题：
分析：首先利用待定系数法可以计算出k的值，再根据k的值即可确定其函数图象所在象限．
解答：解：∵函数y=
k
x
的图象经过点（2，3），
∴k=2×3=6，
∵k=6＞0，
∴图象应在第一、三象限，
故选：A．
点评：此题主要考查了反比例函数图象上点的坐标特征，以及反比例函数图象的性质，关键是掌握凡是函数图象经过的点，比能满足解析式．
练习册系列答案
相关题目
解方程：
x+1
x
+
x
x-1
=2．
已知抛物线y=3ax2+2bx+c，
（1）若a=b=1，且当-1＜x＜1时，抛物线与x轴有且只有一个公共点，求c的取值范围；
（2）若a+b+c=0，且当x=0时，对应的y＞0；当x=1时，对应的y＞0，试判断当0＜x＜1时，抛物线与x轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．
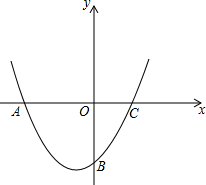如图在平面直角坐标系中，已知抛物线y=
1
2
x2+bx+c经过A（-4，0），B（0，-4），点P（-6，0）在x轴上，点Q为平面内一点（不与A，C重合），且△ACQ是以AC为斜边的直角三角形，连接PQ，设直线PQ与x轴所夹的锐角为α．
（1）求抛物线的函数关系式；
（2）当a＜0时，点P（a，y1），Q（a-1，y2）在抛物线上，比较y1，y2大小；
（3）当α最大时，求点Q的坐标．
（1）(
-2x
3y
)2=
 
  
（2）(-
1
2
)-3=
 
  
（3）（π-6）0=
 
．
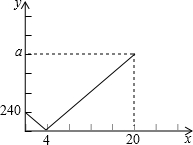A、B与C三地依次在一条直线上．甲，乙两人同时分别从A，B两地沿直线匀速步行到C地，甲到达C地花了20分钟．设两人出发x（分钟）时，甲离B地的距离为y（米），y与x的函数图象如图所示．
（1）甲的速度为
 
米/分钟，a=
 
，A地离C地的距离为
 
米；
（2）已知乙的步行速度是40米/分钟，设乙步行时与B地的距离为y1（米），直接写出y1与x的函数关系式，并在图中画出y1（米）与x（分钟）的大致函数图象（友情提醒：标出线段的端点坐标）；
（3）乙出发几分钟后两人在途中相遇？
已知关于x的一元二次方程2x2-4nx-2n=1和x2-（3n-1）x+2n2-3n=2，问是否存在这样的n值，使得第一个方程的两实根的平方和等于第二个方程的一整数根？若存在，求出这样的n值；若不存在，请说明理由．
某电器经营业主计划购进一批同种型号的空调和电风扇，若购进8台空调和20台电风扇，需要资金17400元；若购进10台空调和30台电风扇，需要资金22500元．
（1）空调和电风扇每台的采购价各是多少元？
（2）此时，由于国家大力推行家电下乡政策，每台空调可以比采购价下调13%，每台电风扇可以比采购价下调10%，该业主计划用23000元购进两种电器共20台，其中空调不少于14台，该业主能否实现购买计划？
已知抛物线y=x2+ax+b与x轴的两个不同的交点A．B距离原点都大于1且小于2，一个直角三角形的两条直角边长分别为a．b，则斜边c的取值范围是（　　）
A、4＜c＜25
B、2＜c＜5
C、5＜c＜32
D、
5
＜c＜4
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网