题目内容
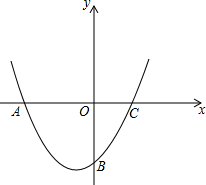 如图在平面直角坐标系中,已知抛物线y=
如图在平面直角坐标系中,已知抛物线y=| 1 |
| 2 |
(1)求抛物线的函数关系式;
(2)当a<0时,点P(a,y1),Q(a-1,y2)在抛物线上,比较y1,y2大小;
(3)当α最大时,求点Q的坐标.
考点:二次函数综合题
专题:
分析:(1)将A(-4,0),B(0,-4)代入抛物线的解析式y=
x2+bx+c,运用待定系数法即可求解;
(2)先将P,Q的坐标代入(1)的抛物线解析式中,可得出y1、y2的表达式,计算y1-y2,然后看得出的结果中在x的不同取值范围下,y1、y2的大小关系;
(3)先由△ACQ是以AC为斜边的直角三角形,得出点Q在以AC为直径的圆D上;再解方程
x2+x-4=0,得到C点的坐标为(2,0),则⊙D的半径为3,点D的坐标为(-1,0);再连接DQ,当α最大时,得到PQ为⊙D的切线,由切线的性质得到∠PQD=90°,根据勾股定理求出PQ=4;过点Q作QE⊥x轴于点E,然后根据锐角三角函数的定义分别求出QE=
,PE=
,进而得到点Q的坐标,注意点Q可以在第二象限,也可以在第三象限.
| 1 |
| 2 |
(2)先将P,Q的坐标代入(1)的抛物线解析式中,可得出y1、y2的表达式,计算y1-y2,然后看得出的结果中在x的不同取值范围下,y1、y2的大小关系;
(3)先由△ACQ是以AC为斜边的直角三角形,得出点Q在以AC为直径的圆D上;再解方程
| 1 |
| 2 |
| 12 |
| 5 |
| 16 |
| 5 |
解答:解:(1)∵抛物线y=
x2+bx+c经过A(-4,0),B(0,-4),
∴
,
解得
,
∴抛物线的函数关系式为y=
x2+x-4;
(2)∵点P(a,y1),Q(a-1,y2)都在该抛物线上,
∴y1-y2=(
a2+a-4)-[
(a-1)2+(a-1)-4]=a+
.
当a+
>0,即-
<a<0时,y1>y2,
当a+
=0,即a=-
时,y1=y2,
当a+
<0,即a<-
时,y1<y2;
 (3)如图.
(3)如图.
∵△ACQ是以AC为斜边的直角三角形,
∴点Q在以AC为直径的圆上.
设AC的中点为D,则⊙D的直径为AC.
∵抛物线y=
x2+x-4与x轴交于点A、C,且A(-4,0),
解方程
x2+x-4=0,得x=-4或2,
∴C(2,0),
∴AC=6,⊙D的半径为3,点D的坐标为(-1,0).
连接DQ,当α最大时,PQ为⊙D的切线,∠PQD=90°,DQ=3.
在△PQD中,∵∠PQD=90°,DQ=3,PD=-1-(-6)=5,
∴PQ=
=4.
过点Q作QE⊥x轴于点E.
∵sin∠QPE=
=
,cos∠QPE=
=
,
∴QE=
=
=
,PE=
=
,
∴OE=OP-PE=6-
=
.
当点Q在第二象限时,Q(-
,
);
当点Q在第三象限时,Q(-
,-
).
综上可知,当α最大时,点Q的坐标为(-
,
)或(-
,-
).
| 1 |
| 2 |
∴
|
解得
|
∴抛物线的函数关系式为y=
| 1 |
| 2 |
(2)∵点P(a,y1),Q(a-1,y2)都在该抛物线上,
∴y1-y2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当a+
| 1 |
| 2 |
| 1 |
| 2 |
当a+
| 1 |
| 2 |
| 1 |
| 2 |
当a+
| 1 |
| 2 |
| 1 |
| 2 |
 (3)如图.
(3)如图.∵△ACQ是以AC为斜边的直角三角形,
∴点Q在以AC为直径的圆上.
设AC的中点为D,则⊙D的直径为AC.
∵抛物线y=
| 1 |
| 2 |
解方程
| 1 |
| 2 |
∴C(2,0),
∴AC=6,⊙D的半径为3,点D的坐标为(-1,0).
连接DQ,当α最大时,PQ为⊙D的切线,∠PQD=90°,DQ=3.
在△PQD中,∵∠PQD=90°,DQ=3,PD=-1-(-6)=5,
∴PQ=
| PD2-DQ2 |
过点Q作QE⊥x轴于点E.
∵sin∠QPE=
| QE |
| PQ |
| DQ |
| PD |
| PE |
| PQ |
| PQ |
| PD |
∴QE=
| PQ•DQ |
| PD |
| 4×3 |
| 5 |
| 12 |
| 5 |
| PQ2 |
| PD |
| 16 |
| 5 |
∴OE=OP-PE=6-
| 16 |
| 5 |
| 14 |
| 5 |
当点Q在第二象限时,Q(-
| 14 |
| 5 |
| 12 |
| 5 |
当点Q在第三象限时,Q(-
| 14 |
| 5 |
| 12 |
| 5 |
综上可知,当α最大时,点Q的坐标为(-
| 14 |
| 5 |
| 12 |
| 5 |
| 14 |
| 5 |
| 12 |
| 5 |
点评:本题主要考查了运用待定系数法求函数的解析式,二次函数的性质,圆周角定理,勾股定理,切线的性质,锐角三角函数的定义,综合性较强,有一定难度.运用差比法比较两个代数式的大小是一种常用的方法;(3)中根据圆周角定理得出点Q在以AC为直径的圆D上及根据切线的性质得出当α最大时,PQ为⊙D的切线是解题的关键.

练习册系列答案
相关题目
若P为质数,且P2+13仍为质数,则P3+25为( )
| A、质数 | B、合数 |
| C、能为质数,也可能为合数 | D、无法确定 |
已知函数y=
的图象经过点(2,3),那么图象应在( )
| k |
| x |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、四象限 |
| D、第三、四象限 |
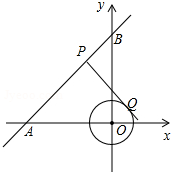 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( ) 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C). 某校兴趣小组坐游轮拍摄瓯江两岸美景.如图,游轮出发点A与江心屿B的距离为300m.在一处测得江心屿B位于A的北偏东30°方向.游轮沿正北方向行驶一段时间后到达C.在C处测得江心屿B位于C的北偏东60°方向.求此时游轮与江心屿之间的距离BC (结果保留整数).
某校兴趣小组坐游轮拍摄瓯江两岸美景.如图,游轮出发点A与江心屿B的距离为300m.在一处测得江心屿B位于A的北偏东30°方向.游轮沿正北方向行驶一段时间后到达C.在C处测得江心屿B位于C的北偏东60°方向.求此时游轮与江心屿之间的距离BC (结果保留整数).