题目内容
5. 将矩形ABCD对折,设折痕为MN,再把B点叠在折痕线MN上点B′,若AB=$\sqrt{3}$,折痕AE的长为2.
将矩形ABCD对折,设折痕为MN,再把B点叠在折痕线MN上点B′,若AB=$\sqrt{3}$,折痕AE的长为2.
分析 由平分线分线段成比例定理可知:EB′=FB′,然后可证明△AEB′≌△AFB′,于是得到∠B′AE=∠B′AD.由折叠可得∠EAB′=∠BAE,那么组成直角的三个角相等,每个角都为30°,最后再△ABE中,利用特殊锐角三角函数值可求得AE的长.
解答  解:如图所示:延长EB′与AD交于点F.
解:如图所示:延长EB′与AD交于点F.
∵∠AB′E=∠B=90°,MN是对折折痕,
∴EB′=FB′,∠AB′E=∠AB′F.
在△AEB′和△AFB′,$\left\{\begin{array}{l}{AB′=AB′}\\{∠AB′E=∠AB′F}\\{EB′=FB′}\end{array}\right.$,
∴△AEB′≌△AFB′.
∴∠B′AE=∠B′AD.
由翻折的性质可知:∠BAE=∠EAB′,
∴∠BAE=∠EAB′=∠B′AF=30°
∴AE=AB÷cos30°=$\sqrt{3}÷\frac{\sqrt{3}}{2}$=2.
∴AE=2.
故答案为:2.
点评 本题主要考查的是翻折的性质、全等三角形的性质和判定、平行线分线段成比例定理,特殊锐角三角函数值,求得∠BAE=30°是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
16.代数式$\frac{{\sqrt{x-1}}}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥2 | B. | x≥1 | C. | x≠2 | D. | x≥1且x≠2 |
 如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS.
如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS. 如图,在等腰三角形ABC中,AB=AC,BD是AC边的高,求证:BC2=2CA•CD.(提示:过点A作AE⊥BC于点E)
如图,在等腰三角形ABC中,AB=AC,BD是AC边的高,求证:BC2=2CA•CD.(提示:过点A作AE⊥BC于点E)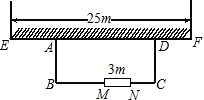 利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.
利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米. 如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.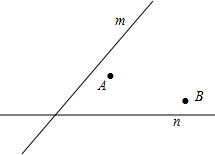 如图,电信部门要在S区修建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?(保留作图痕迹)
如图,电信部门要在S区修建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?(保留作图痕迹) 如图,抛物线y=$\frac{1}{2}$x2+k与扇形OAB的边界总有两个交点,则实数k的取值范围是-2<k<$\frac{1}{2}$.
如图,抛物线y=$\frac{1}{2}$x2+k与扇形OAB的边界总有两个交点,则实数k的取值范围是-2<k<$\frac{1}{2}$.