题目内容
10. 如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD:OA=OE:OB.
分析 根据平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似可以得出比例式,等量代换即可得到结论.
解答 证明:∵DF∥AC,EF∥BC,
∴△ODF∽△OAC,△OEF∽△OBC,
∴$\frac{OD}{OA}=\frac{OF}{OC}$,$\frac{OE}{OB}=\frac{OF}{OC}$,
∴OD:OA=OE:OB.
点评 本题考查了平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似的判定方法的运用,相似三角形的性质的运用,相似三角形的判定的运用,解答时证明三角形相似是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
15.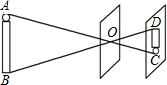 在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
 在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
在小孔成像问题中,根据如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )| A. | 3倍 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2倍 |
20.已知$\sqrt{a+2}$+(b-1)2=0,则(a+b)2015的值是( )
| A. | -1 | B. | 1 | C. | 2015 | D. | -2015 |
 如图所示,根据数轴上各点的位置,写出它们所表示的数.
如图所示,根据数轴上各点的位置,写出它们所表示的数. 将矩形ABCD对折,设折痕为MN,再把B点叠在折痕线MN上点B′,若AB=$\sqrt{3}$,折痕AE的长为2.
将矩形ABCD对折,设折痕为MN,再把B点叠在折痕线MN上点B′,若AB=$\sqrt{3}$,折痕AE的长为2.