题目内容
15.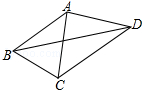 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )| A. | 110° | B. | 88° | C. | 84° | D. | 66° |
分析 首先以A为圆心,AB长为半径画弧,然后可确定B、C、D同在⊙A上,再根据∠CBD=2∠BDC可得$\widehat{CD}$=2$\widehat{BC}$,然后可得∠CAD=2∠BAC=84°.
解答  解:以A为圆心,AB长为半径画弧,
解:以A为圆心,AB长为半径画弧,
∵AB=AC=AD,
∴B、C、D同在⊙A上,
∵∠CBD=2∠BDC,
∴$\widehat{CD}$=2$\widehat{BC}$,
∴∠CAD=2∠BAC=84°,
故选:C.
点评 此题主要考查了圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
6.下列各组中,是同类项的是( )
| A. | 3x2y与3xy2 | B. | 3xy与-2xy2 | C. | -2xy2与-2ab2 | D. | 0与π |
20.一个三角形三个内角的度数之比为1:2:3,则这个三角形一定是( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
5.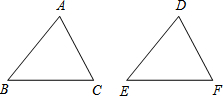 如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
 如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )| A. | ∠B=∠E | B. | BC=EF | C. | ∠C=∠F | D. | AC=DF |
 (1)用适当的语句表述图中的点A、B与直线l的关系;
(1)用适当的语句表述图中的点A、B与直线l的关系;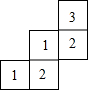 由一些棱长为1的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图和左视图(先用铅笔作出草图,确认无误后,再用签字笔勾线).
由一些棱长为1的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图和左视图(先用铅笔作出草图,确认无误后,再用签字笔勾线).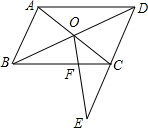 如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )