题目内容
15.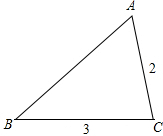 定义:如果两条线段将一个三角形分割成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图,△ABC中,AC=2,BC=3,∠C=2∠B
定义:如果两条线段将一个三角形分割成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图,△ABC中,AC=2,BC=3,∠C=2∠B(1)请在图中画出△ABC的三分线,并简单说明你作图方法.
(2)请直接写出两条三分线的长度.
分析 (1)因为∠C=2∠B,作∠C的角平分线,则可得第一个等腰三角形.而后借用圆规,以边长画弧,根据交点,寻找是否存在三分线,易得图形为三分线;
(2)根据外角等于内角之和及腰相等等情况列出等量关系,求解方程可知各线的长.
解答 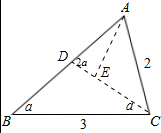 解:(1)如图,①作∠C的角平分线,则可得第一个等腰三角形△DBC;
解:(1)如图,①作∠C的角平分线,则可得第一个等腰三角形△DBC;
②以AD边长画弧,交DC于点E,如图CD、AE就是所求的三分线.
(2)如图,
设∠B=α,则∠DCB=∠DCA=∠EAC=α,∠ADE=∠AED=2α,
此时△AEC∽△BDC,△ACD∽△ABC,
设AE=AD=x,BD=CD=y,
∵△AEC∽△BDC,
∴x:y=2:3,
∵△ACD∽△ABC,
∴2:x=(x+y):2,
所以联立得方程组:$\left\{\begin{array}{l}{x:y=2;3}\\{2:x=(x+y):2}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=\frac{2}{5}\sqrt{10}}\\{y=\frac{3}{5}\sqrt{10}}\end{array}\right.$,
即三分线长分别是$\frac{2}{5}$$\sqrt{10}$和$\frac{3}{5}$$\sqrt{10}$.
点评 本题考查了复杂作图以及等腰三角形知识、相似三角形的判定与性质等知识,得出△AEC∽△BDC、△ACD∽△ABC是解题关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
7.一元二次方程x2+2=0的根的情况为( )
| A. | 没有实根 | B. | 有两个相等的实根 | ||
| C. | 有两个不等的实根 | D. | 有两个实根 |
6.下列运算中,正确的是( )
| A. | b3•b3=b9 | B. | (-x3y)•(xy2)=x4y3 | C. | (-2x3)2=-4x6 | D. | (-a2)3=-a6 |
10.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h(单位:km)表示距离地面的高度,用T(单位:℃)表示温度,T如何随着h的变化而变化?写出T随着h随着h变化的函数解析式;
(2)画出函数图象;
(3)你能预测出距离地面6km的高空温度是多少吗?
| 距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
(1)如果用h(单位:km)表示距离地面的高度,用T(单位:℃)表示温度,T如何随着h的变化而变化?写出T随着h随着h变化的函数解析式;
(2)画出函数图象;
(3)你能预测出距离地面6km的高空温度是多少吗?
7.在△ABC中,已知∠A=60°,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,则△ABC是( )
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
4.森林是地球之肺,每年平均能为人类提供大约28.3亿吨的有机物,十年所提供的有机物用科学记数法表示为( )
| A. | 2.83×107吨 | B. | 2.83×108吨 | C. | 2.83×109吨 | D. | 2.83×1010吨 |
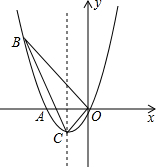 已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C
已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C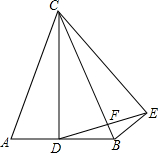 已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF.
已知AC=BC,DC=EC,∠BCA=∠DCE,CD⊥AB,求证:∠BCE=∠BEF.