题目内容
1. 如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.
如图,分别以△ABC的三边为边,在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR,连接PA,AQ,QR,RP,那么四边形PRQA是平行四边形吗?证明你的结论.
分析 可先证明∠1=∠2,再根据等边三角形的性质可得PB=AB,BC=RB,利用SAS可判定△ABC≌△PBR,进而可得PR=AC,同理可证出AP=QR.进而可得四边形PRQA是平行四边形.
解答 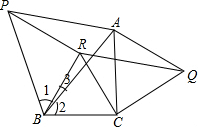 解:四边形PRQA是平行四边形,
解:四边形PRQA是平行四边形,
理由:∵△ABP,△BCR都是等边三角形,
∴∠PBA=∠RBC=60°,AB=PB,BC=RB,
∴∠1=∠2=60°-∠ABR,
在△ABC和△PRB中,
$\left\{\begin{array}{l}{PB=AB}\\{∠1=∠2}\\{RB=BC}\end{array}\right.$,
∴△ABC≌△PBR(SAS).
∴PR=AC.
∵△ACQ是等边三角形,
∴AC=AQ,
∴PR=AQ.
同理可得AP=QR.
∴四边形PRQA是平行四边形.
点评 本题主要考查了等边三角形的性质,平行四边形的判定,关键是掌握等边三角形三边相等,三个角都是60°,两组对边分别相等的四边形是平行四边形.

练习册系列答案
相关题目
 如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形 ABCD 的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5. 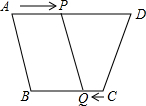 如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形? 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,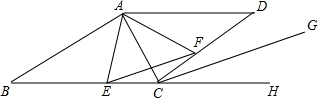

 如图,在边长为4的正方形ABCD中,以BC为直径的半圆交对角线BD于E,则图中阴影部分的面积为8.
如图,在边长为4的正方形ABCD中,以BC为直径的半圆交对角线BD于E,则图中阴影部分的面积为8.