题目内容
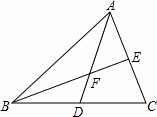
在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为( )
A.8,3 B.8,6 C.4,3 D.4,6
A
考点:等腰三角形的判定;相似三角形的判定与性质.
分析:根据已知可证△ABC∽△DEF,且△ABC和△DEF的相似比为2,再根据相似三角形周长的比等于相似比,面积的比等于相似比的平方即可求△DEF的周长、面积.
解答: 解:因为在△ABC和△DEF中,AB=2DE,AC=2DF,
∴ =2,
=2,
又∵∠A=∠D,
∴△ABC∽△DEF,且△ABC和△DEF的相似比为2,
∵△ABC的周长是16,面积是12,
∴△DEF的周长为16÷2=8,面积为12÷4=3,

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

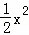 ﹣x+
﹣x+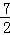 .
.