题目内容
8.对于抛物线y=ax2+bx+c,下列命题中正确的是( )①若a+b+c=0,则抛物线与x轴一定有公共点;
②若b=2a+5c,则抛物线与x轴有两个公共点;
③若b=a+c,则抛物线与x轴一定有两个公共点;
④b2-4ac>0,则抛物线的图象与坐标轴的公共点的个数是2或3.
| A. | 只有①②③ | B. | 只有①③④ | C. | 只有①②④ | D. | 只有②③④ |
分析 根据△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.即可一一判断.
解答 解:①正确.∵△=b2-4ac=(-a-c)2-4ac=(a-c)2≥0,
∴抛物线与x轴一定有公共点;
②正确.∵△=b2-4ac=(2a+5c)2-4ac=4a2+16ac+25c2=4(a+2c)2+9c2(a-c)2>0,
∴抛物线与x轴有两个公共点.
③错误.∵△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,
∴抛物线与x轴可能有两个公共点也可能有一个公共点.
④正确.∵b2-4ac>0,∴抛物线的图象与坐标轴的公共点的个数是3个或2个(经过原点时).
故选C.
点评 本题考查抛物线与x轴的交点,二次函数的图象与系数关系,考查学生学生对抛物线及根的判别式应用知识点的掌握.此题主要利用了二次函数y=ax2+bx+c的图象与x轴交点的个数的判断,灵活应用根的判别式是解题的关键.

练习册系列答案
相关题目
16.若$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$,则$\frac{2{a}^{2}-3bc+{c}^{2}}{{a}^{2}-2ab-{c}^{2}}$的值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.运用等式性质的变形,正确的是( )
| A. | 如果$\frac{a}{2}$=$\frac{b}{2}$,那么a=b | B. | 如果x=y,那么$\frac{x}{a}$=$\frac{y}{a}$ | ||
| C. | 如果mx=my,那么x=y | D. | 如果a=b,那么a+c=b-c |
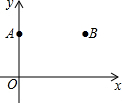 如图,已知点A(0,4)、点B(6,4),点C在x轴上,若△ABC是等腰三角形,则点C的横坐标为$6-2\sqrt{5}$或$6+2\sqrt{5}$或3或$-2\sqrt{5}$或$2\sqrt{5}$.
如图,已知点A(0,4)、点B(6,4),点C在x轴上,若△ABC是等腰三角形,则点C的横坐标为$6-2\sqrt{5}$或$6+2\sqrt{5}$或3或$-2\sqrt{5}$或$2\sqrt{5}$.