题目内容
8.如图a是长方形纸带,∠BFE=15°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是135°.
分析 根据长方形纸条的特征---对边平行,利用平行线的性质和翻折不变性求出∠2=∠EFG,继而求出∠GFC的度数,再减掉∠GFE即可得∠CFE的度数.
解答 解:如图,
延长AE到H,由于纸条是长方形,
∴EH∥GF,
∴∠1=∠EFG,
根据翻折不变性得∠1=∠2,
∴∠2=∠EFG,
又∵∠DEF=15°,
∴∠2=∠EFG=15°,
∠FGD=15°+15°=30°.
在梯形FCDG中,
∠GFC=180°-30°=150°,
根据翻折不变性,∠CFE=∠GFC-∠GFE=150°-15°=135°.
故答案为:135°.
点评 此题考查了翻折变换,要充分利用长方形纸条的性质和翻折不变性解题.从变化中找到不变量是解题的关键.

练习册系列答案
相关题目
19.下列命题是真命题的是( )
| A. | 同位角相等 | B. | 平行于同一直线的两条直线平行 | ||
| C. | 点(2,3)在直线y=2x+3上 | D. | 函数y=-x+1中y随x的增大而增大 |
11.下列数轴画法正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为10cm.
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为10cm.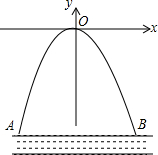 某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.
某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.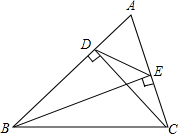 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.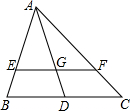 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G. 已知:∠A+∠C=∠B=60°,AD=CE,求证:BE=CD.
已知:∠A+∠C=∠B=60°,AD=CE,求证:BE=CD.