题目内容
如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为6m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（ ）| A、AB=12m |
| B、MN∥AB |
| C、△CMN∽△CAB |
| D、CM：MA=1：2 |
考点：三角形中位线定理
专题：
分析：根据三角形的中位线定理，三角形的中位线平行于第三边且等于第三边的一半即可作出判断．
解答：解：∵M、N是AC和BC的中点，
∴MN∥AB，且MN=
AB，CM：MA=1：1．
则AB=2MN=2×6=12（m）．
故A、B都正确，D错误；
∵MN∥AB，
∴△CMN∽△CAB，故C正确．
故选D．
∴MN∥AB，且MN=
| 1 |
| 2 |
则AB=2MN=2×6=12（m）．
故A、B都正确，D错误；
∵MN∥AB，
∴△CMN∽△CAB，故C正确．
故选D．
点评：本题考查了三角形的中位线定理以及相似三角形相似的判断，理解定理的内容是关键．
练习册系列答案
相关题目
如图，已知点C是以AB为直径的半圆上的动点，AB=10；连结BC、AC，并延长AC至点D，使DC=AC，过D作DE⊥AB于E，ED交BC于点F．
如图，正方形ABCD中，对角线AC、BD交于O，BE平分∠DBC交AC于F，交DC于E，求证：OF=二元一次方程组
的解是（ ）
|
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
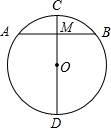如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知AB=8，CM=2，求直径CD的长．
如图，直线a、b被直线c所截，若a∥b，∠3=60°，∠2=75°，则∠1的大小是（ ）| A、120° | B、130° |
| C、135° | D、150° |