题目内容
3.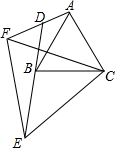 如图,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连结AF和BE,如果直线EB交直线AF于点D.
如图,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连结AF和BE,如果直线EB交直线AF于点D.(1)求证:AF=BE;
(2)当△CEF绕点C旋转时,∠ADB的大小是否发生变化?(直接给出答案)
分析 (1)根据题中所给的等边三角形的条件,两对边对应相等,有一个角都等于60°-∠FBC,利用SAS证AF和BE所在的三角形全等即可;
(2)∠ADB的大不变化,由(1)中的全等三角形可知∠AFC=∠BEC,再根据等边三角形的性质以及三角形外角和定理可求出∠ADB=120°,是一个定值,即不发生变化.
解答 (1)证明:在△AFC和△BEC中,
∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠ECF=60°,
∴∠ACF=60°-∠BCF,∠BCE=60°-∠BCF,
∴∠ACF=∠BCE,
在△AFC与△BEC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACF=∠BCE}\\{CF=CE}\end{array}\right.$,
∴△AFC≌△BEC(SAS),
∴AF=BE;
(2)∠ADB的大不变化,理由如下:
∵△AFC≌△BEC,
∴∠AFC=∠BEC,
∴∠AFC+∠FED=∠BEC+∠EFD=60°
∵∠ADB=∠DFE+∠FED,
∴∠ADB=∠AFC+60°+∠FED=120°,
即∠ADB的大不变化.
点评 本题主要考查旋转的性质:旋转前后图形的大小和形状不变,只是位置发生了变化.证两条线段相等,通常是证这两条线段所在的两个三角形全等,类似的题,证明方法基本不变.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
11.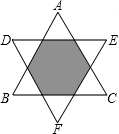 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
8.计算(m3n)2的结果是( )
| A. | m6 | B. | m6n2 | C. | m3n2 | D. | m5n2 |
15.若9x2-kxy+49y2是一个完全平方式,那么k的值是( )
| A. | 42 | B. | -42 | C. | ±21 | D. | ±42 |