题目内容
10.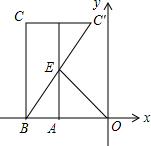 如图,已知点A的坐标为(m,0),点B的坐标为(m-2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为(-2,2).
如图,已知点A的坐标为(m,0),点B的坐标为(m-2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为(-2,2).
分析 先根据矩形的性质与轴对称的性质得出AB=C′D,再利用AAS证明△ABE≌△DC′E,得出AE=DE=-m.根据△BOE的面积为4,列出方程$\frac{1}{2}$(2-m)(-m)=4,解方程即可.
解答 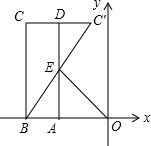 解:如图,设AE与CC′交于点D.
解:如图,设AE与CC′交于点D.
∵点A的坐标为(m,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,
∴CB=-2m.
∵点C,C′关于直线x=m对称,
∴CD=C′D,
∵ABCD是矩形,AB=CD,
∴AB=C′D.
又∵∠BAE=∠C′DE=90°,∠AEB=DEC′,
∴△ABE≌△DC′E,
∴AE=DE,
∴AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC=-m.
∵△BOE的面积为4,
∴$\frac{1}{2}$(2-m)(-m)=4,
整理得,m2-2m-8=0,
解得m=4或-2,
∵在x轴上方取点C,
∴-2m>0,
∴m<0,
∴m=4不合题意舍去,
∵点E的坐标为(m,-m),
∴点E的坐标为(-2,2).
故答案为(-2,2).
点评 本题考查了矩形的性质,轴对称的性质,全等三角形的判定与性质,三角形的面积,得出AE=DE=-m是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论: 如图,已知⊙O经过点A(2,0)、C(0,2),直线y=kx与⊙O分别交于点B、D,则四边形ABCD面积的最大值为4$\sqrt{2}$.
如图,已知⊙O经过点A(2,0)、C(0,2),直线y=kx与⊙O分别交于点B、D,则四边形ABCD面积的最大值为4$\sqrt{2}$.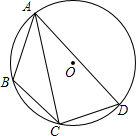 在⊙O的内接四边形ABCD中,AB=6,AD=10,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{16}{3}$$\sqrt{3}$.
在⊙O的内接四边形ABCD中,AB=6,AD=10,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{16}{3}$$\sqrt{3}$. 如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1,S2,若S1=2,S2=3,AB2=5,则△ABC的形状是直角三角形.
如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1,S2,若S1=2,S2=3,AB2=5,则△ABC的形状是直角三角形.