题目内容
1.如果a=2$\sqrt{2}$+3,b=2$\sqrt{2}$-3,那么( )| A. | a=$\frac{1}{b}$ | B. | a=-$\frac{1}{b}$ | C. | a=b | D. | a=-b |
分析 结合分母有理化的概念:分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式,进行求解即可.
解答 解:∵a=2$\sqrt{2}$+3,b=2$\sqrt{2}$-3,
∴ab=(2$\sqrt{2}$+3)(2$\sqrt{2}$-3)
=8-9
=-1.
∴a=-$\frac{1}{b}$.
故选B.
点评 本题考查了分母有理化,解答本题的关键在于熟练掌握分母有理化的概念:分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
相关题目
11. 有一条直的宽纸带折叠成如图所示,则∠1的度数为( )
有一条直的宽纸带折叠成如图所示,则∠1的度数为( )
 有一条直的宽纸带折叠成如图所示,则∠1的度数为( )
有一条直的宽纸带折叠成如图所示,则∠1的度数为( )| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
12.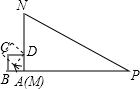 如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
 如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )| A. | $\frac{7π}{3}$+2 | B. | 2π+2 | C. | $\frac{7π}{3}$ | D. | $\frac{4π}{3}$ |
9.平面直角坐标系中,P(-2a-6,a-4)在第三象限,则a的取值范围是( )
| A. | a>4 | B. | a≥-12 | C. | -3≤a<4 | D. | -3<a<4 |
16.下列说法中正确的是( )
| A. | 0是最小的整数 | B. | 最大的负有理数是-1 | ||
| C. | 两个负数绝对值大的负数小 | D. | 有理数a的倒数是$\frac{1}{a}$ |
6.一个正方形的面积为2,则其边长可估算为( )
| A. | 1.2与1.3之间 | B. | 1.3与1.4之间 | C. | 1.4与1.5之间 | D. | 1.5与1.6之间 |
10.下列图形中有稳定性的是( )
| A. | 正方形 | B. | 长方形 | C. | 平行四边形 | D. | 等边三角形 |