题目内容
12.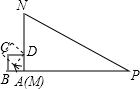 如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )| A. | $\frac{7π}{3}$+2 | B. | 2π+2 | C. | $\frac{7π}{3}$ | D. | $\frac{4π}{3}$ |
分析 第一次翻滚:绕D,点A围成的扇形是圆心角是90°,半径是1;
第二次翻滚:绕C,点A围成的图形是扇形和两个三角形,扇形是圆心角是90°,半径是$\sqrt{2}$,两个等腰直角三角形组成一个边长为1的正方形;
第三次翻滚:绕B,点A围成的扇形是圆心角是210°,半径是1;
第四次翻滚:绕A,点A不动;
第五次翻滚:绕D,点A围成的扇形是圆心角是90°,半径是1;
…
依次重复,直到第八次翻滚结束.
解答 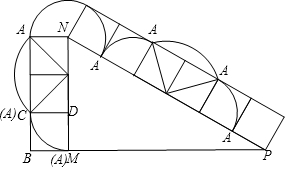 解:如图,
解:如图,
点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积:
S=$\frac{90π×{1}^{2}}{360}$×3+$\frac{90π×(\sqrt{2})^{2}}{360}$×2+$\frac{210π×{1}^{2}}{360}$+2
=$\frac{π}{4}$×3+$\frac{π}{2}$×2+$\frac{7π}{12}$+2
=$\frac{7π}{3}$+2.
点评 本题考查了点的轨迹的问题,考查了正方形的性质和翻滚的性质,正方形的边长相等,且每一个角都是90°,熟练掌握扇形面积公式:S=$\frac{nπ{R}^{2}}{360}$(n是圆心角的度数,R是扇形的半径);此类点的轨迹题比较难,关键是正确画出图形,有空间想象能力,动手操作,得出结论.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
2.化简x+y-(x-y)的最后结果是( )
| A. | 2x+2y | B. | 2y | C. | 2x | D. | 0 |
20.已知抛物线y=a(x+2m)2+m(a≠0,a,m为常数),当m取不同的实数时,其顶点在某函数图象上移动,则该函数是下列函数中的( )
| A. | y=$\frac{1}{2}$x | B. | y=2x | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{1}{2}$x |
7.矩形具有而菱形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 是中心对称图形 |
17.如果x-y=5且y-z=5,那么x-z的值是( )
| A. | 5 | B. | 10 | C. | -5 | D. | -10 |
4. 如图,直线a、b被直线c所截,a∥b,∠2=∠3,若∠1=78°,则∠4等于( )
如图,直线a、b被直线c所截,a∥b,∠2=∠3,若∠1=78°,则∠4等于( )
 如图,直线a、b被直线c所截,a∥b,∠2=∠3,若∠1=78°,则∠4等于( )
如图,直线a、b被直线c所截,a∥b,∠2=∠3,若∠1=78°,则∠4等于( )| A. | 38° | B. | 39° | C. | 40° | D. | 41° |
1.如果a=2$\sqrt{2}$+3,b=2$\sqrt{2}$-3,那么( )
| A. | a=$\frac{1}{b}$ | B. | a=-$\frac{1}{b}$ | C. | a=b | D. | a=-b |
2.下列说法不正确的是( )
| A. | 若ab=1,则a与b互为倒数 | B. | 若ab<0,则$\frac{a}{b}$<0 | ||
| C. | 若a+b=0,则$\frac{a}{b}$=-1 | D. | 若$\frac{a}{b}$>0,则ab>0 |
 如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4=135度.
如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4=135度.