题目内容
9. 如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工,为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂直线l,过点B作一直线(在山的旁边经过),与了相交于D点,经测量∠ABD=135°,BD=800米,应在直线l上距离D点566米的C处开挖($\sqrt{2}≈$1.414,精确到1米).
如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工,为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂直线l,过点B作一直线(在山的旁边经过),与了相交于D点,经测量∠ABD=135°,BD=800米,应在直线l上距离D点566米的C处开挖($\sqrt{2}≈$1.414,精确到1米).
分析 首先证明△BCD是等腰直角三角形,再根据勾股定理可得CD2+BC2=BD2,然后再代入BD=800米进行计算即可.
解答 解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△DCB中:CD2+BC2=BD2,
2CD2=8002,
CD=400$\sqrt{2}$≈566(米),
答:直线L上距离D点566米的C处开挖.
故答案为566米.
点评 此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
20.下列命题是真命题的是( )
| A. | 垂线段最短 | |
| B. | 垂直于同一条直线的两直线平行 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 两条直线不平行则相交 |
4.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是$±\frac{1}{5}$ | B. | -9是81的一个平方根 | ||
| C. | 0.2的算术平方根是0.04 | D. | -27没有平方根 |
14.二次函数y=2(x+2)2-4的最小值是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
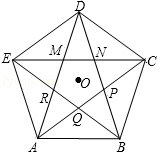 如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为$\frac{\sqrt{5}-1}{2}$.若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.
如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR.图中有很多顶角为36°的等腰三角形,我们把这种三角形称为“黄金三角形”,黄金三角形的底与腰之比为$\frac{\sqrt{5}-1}{2}$.若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.