题目内容
11.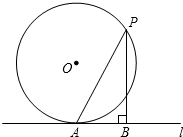 如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )
如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 作直径AC,连接CP,得出△APC∽△PBA,利用$\frac{AP}{AC}$=$\frac{BP}{AP}$,得出m-n=m-$\frac{1}{6}$m2=-$\frac{1}{6}$m2+m=-$\frac{1}{6}$(m-3)2$+\frac{3}{2}$,所以m-n的最大值是$\frac{3}{2}$.
解答 解:如图,作直径AC,连接CP,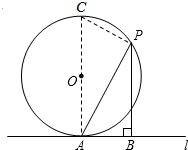
∴∠CPA=90°,
∵AB是切线,
∴CA⊥AB,
∵PB⊥l,
∴AC∥PB,
∴∠CAP=∠APB,
∴△APC∽△PBA,
∴$\frac{AP}{AC}$=$\frac{BP}{AP}$,
∵PA=m,PB=n,半径为3,
∴$\frac{m}{6}$=$\frac{n}{m}$,
∴n=$\frac{1}{6}$m2,
∴m-n=m-$\frac{1}{6}$m2=-$\frac{1}{6}$m2+m=-$\frac{1}{6}$(m-3)2$+\frac{3}{2}$,
∴m-n的最大值是$\frac{3}{2}$.
故选C.
点评 此题考查了切线的性质,平行线的性质,相似三角形的判定与性质,以及二次函数的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
4.某校计划租用7辆客车,送八年级师生去南湖参观一大会址.现有甲、乙两种型号的客车可供选择,它们的载客量和租金如下表所示.设租用甲种客车x辆,租用总费用为y元.
(1)求出y(元)与x(辆)之间的函数表达式;
(2)若要求租车总费用不超过6500元,问有几种租车方案?哪种方案能使总载客量最大?
| 类别 | 甲种客车 | 乙种客车 |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 1000 | 800 |
(2)若要求租车总费用不超过6500元,问有几种租车方案?哪种方案能使总载客量最大?
5.方程x-$\frac{x-5}{3}$=1,去分母得( )
| A. | 3x-2x+10=1 | B. | x-(x-5)=3 | C. | 3x-(x-5)=3 | D. | 3x-2x+10=6 |
 观察图,回答下列问题:
观察图,回答下列问题: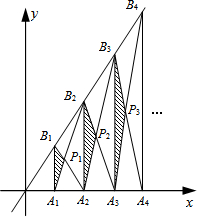 已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.
已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=2x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2 B3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn.若△A1B1P1,△A2B2P2,△A3B3P3,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn为$\frac{{n}^{2}}{2n+1}$.