题目内容
8.已知O为坐标原点,抛物线y1=ax2+bx+c(c<0)与x轴相交于点A(x1,0),B(x2,0).与y轴交于点C,且OC=3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=-3x+t上.(1)求点C的坐标和t的值;
(2)当y1随着x的增大而减小时,求自变量x的取值范围;
(3)若y1>y2,求自变量x的取值范围.
分析 (1)令x=0,则y=c,再根据OC=3,可求点C的坐标,把C(0,-3)代入y2=-3x+t可求t的值;
(2)把A(x1,0)代入,y2=-3x-3,可求A(-1,0),进一步得到B(3,0),再待定系数法可求自变量x的取值范围;
(3)根据两个函数的交点坐标即可得到自变量x的取值范围.
解答 解:(1)令x=0,则y=c,
∴C(0,c),
∵OC=3,
∴|c|=3,即c=±3,
又∵c<0,
∴c=-3,
∴C(0,-3),
把C(0,-3)代入y2=-3x+t,则0+t=-3,即t=-3;
(2)∵t=-3,
∴y2=-3x-3,
把A(x1,0)代入,y2=-3x-3,则-3x1-3=0,即x1=-1,
∴A(-1,0),
∵x1x2异号,x1=-1<0∴x2>0,
∵|x1|+|x2|=4,
∴1+x2=4,x2=3,则B(3,0),
代入${y_1}=a{x^2}+bx-3$得$\left\{\begin{array}{l}a-b-3=0\\ 9a+3b-3=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$,
${y_1}={x^2}-2x-3={(x-1)^2}-4$,
则当x≤1 时,y随x增大而减小.
∴当y随x增大而减小时,x≤1;
(3)若y1>y2,自变量x的取值范围为x<-1或x>0.
点评 此题主要考查了二次函数与不等式(组),抛物线与x轴的交点,以及求两函数的交点坐标以及比较函数值的大小等知识,利用数形结合比较函数值的大小是这部分考查的重点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在一次函数y=(m+1)x+5中,y随x的增大而减小,则m的取值范围是( )
| A. | m<-1 | B. | m>-1 | C. | m=-1 | D. | m<1 |
18.已知a-b=2,b-c=$\frac{1}{2}$,则代数式2(a-c)-2(b-c)的值是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | 4 |
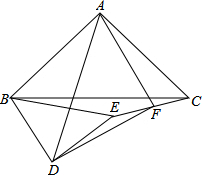 已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形.
已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形.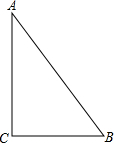 如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.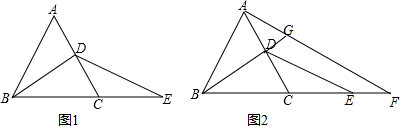
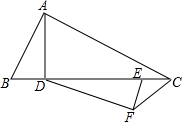 如图,△ABC中,AD为高,∠B=2∠ACB,E为CD上一点,EC=BD,EF∥AB,且E在FC的垂直平分线上,求证:DF⊥EF.
如图,△ABC中,AD为高,∠B=2∠ACB,E为CD上一点,EC=BD,EF∥AB,且E在FC的垂直平分线上,求证:DF⊥EF.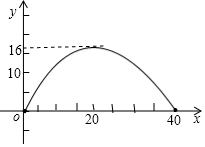 如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.
如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.