Question

18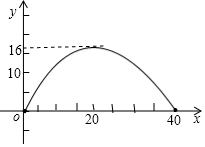．如图建立直角坐标系，某抛物线型桥拱的最大高度为16米，跨度为40米，则它对应的解析式为：y=-$\frac{1}{25}$x²+$\frac{2}{5}$x．

Answer 1

分析 由图象可知抛物线顶点坐标（20，16），经过（0，0），（40，0）．利用顶点式即可解决问题．

解答 解：由图象可知抛物线顶点坐标（20，16），经过（0，0），（40，0）．
设抛物线的解析式为y=a（x-20）²+16，把（0，0）代入得到a=-$\frac{1}{25}$，
∴抛物线的解析式为y=-$\frac{1}{25}$（x-20）²+16，
即y=-$\frac{1}{25}$x²+$\frac{2}{5}$x，
故答案为y=-$\frac{1}{25}$x²+$\frac{2}{5}$x．

点评 本题考查二次函数的应用，解题的关键是灵活应用抛物线的顶点式解决问题，属于中考常考题型．