题目内容
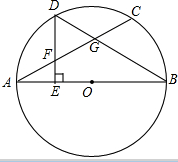 如图,AB是⊙O的直径,C是⊙O上一点,D是
如图,AB是⊙O的直径,C是⊙O上一点,D是 |
| AC |
(1)DF=FG;
(2)AF=FG;
(3)当D为
 |
| ABC |
考点:圆周角定理,等腰三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:(1)连接AD,延长DE交⊙O于M,如图1,根据垂径定理得
=
,而D是
的中点,则
=
=
,根据圆周角定理得到∠3=∠B,再由AB为直径,
得到∠ADB=90°,所以∠3+∠AGD=90°,易得∠1=∠AGD,所以DF=FG;
(2)根据圆周角定理由
=
=
得到∠3=∠2,则AF=FG;
(3)连接AD,延长DE交⊙O于M,如图2,根据垂径定理由DE⊥AB得到
=
,则有
=
=
,于是根据圆周角定理得到∠CAD=∠ADM,所以FA=FD;
再由三角形外角性质得∠ABD=∠G+∠BAC,由
=
得∠ABD=∠CAD=∠BAC+∠DAB,所以∠G=∠BAD,然后利用
=
得到∠BDM=∠BAD,所以∠BDM=∠G,于是可判断FD=FG.
 |
| AD |
 |
| AM |
 |
| AC |
 |
| AD |
 |
| AM |
 |
| CD |
得到∠ADB=90°,所以∠3+∠AGD=90°,易得∠1=∠AGD,所以DF=FG;
(2)根据圆周角定理由
 |
| AD |
 |
| AM |
 |
| CD |
(3)连接AD,延长DE交⊙O于M,如图2,根据垂径定理由DE⊥AB得到
 |
| AD |
 |
| AM |
 |
| AD |
 |
| AM |
 |
| CD |
再由三角形外角性质得∠ABD=∠G+∠BAC,由
 |
| AD |
 |
| CD |
 |
| BD |
 |
| BM |
解答:证明:(1)连接AD,延长DE交⊙O于M,如图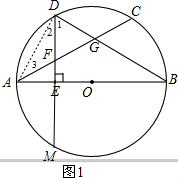 1,
1,
∵DE⊥AB,
∴
=
,
∵D是
的中点,
∴
=
=
,
∴∠3=∠B,
∵AB为直径,
∴∠ADB=90°,
∴∠3+∠AGD=90°,
∵∠B+∠1=90°,
∴∠1=∠AGD,
∴DF=FG;
(2)∵
=
=
,
∴∠3=∠2,
∴AF=FG;
(3)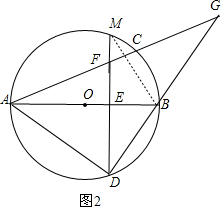 上述两个结论成立.
上述两个结论成立.
连接AD,延长DE交⊙O于M,如图2,
∵DE⊥AB,
∴
=
,
∵D是
的中点,
∴
=
=
,
∴∠CAD=∠ADM,
∴FA=FD;
∵∠ABD=∠G+∠BAC,
而
=
,
∴∠ABD=∠CAD=∠BAC+∠DAB,
∴∠G=∠BAD,
∵
=
,
∴∠BDM=∠BAD,
∴∠BDM=∠G,
∴FD=FG.
 1,
1,∵DE⊥AB,
∴
 |
| AD |
 |
| AM |
∵D是
 |
| AC |
∴
 |
| AD |
 |
| AM |
 |
| CD |
∴∠3=∠B,
∵AB为直径,
∴∠ADB=90°,
∴∠3+∠AGD=90°,
∵∠B+∠1=90°,
∴∠1=∠AGD,
∴DF=FG;
(2)∵
 |
| AD |
 |
| AM |
 |
| CD |
∴∠3=∠2,
∴AF=FG;
(3)
 上述两个结论成立.
上述两个结论成立.连接AD,延长DE交⊙O于M,如图2,
∵DE⊥AB,
∴
 |
| AD |
 |
| AM |
∵D是
 |
| ABC |
∴
 |
| AD |
 |
| AM |
 |
| CD |
∴∠CAD=∠ADM,
∴FA=FD;
∵∠ABD=∠G+∠BAC,
而
 |
| AD |
 |
| CD |
∴∠ABD=∠CAD=∠BAC+∠DAB,
∴∠G=∠BAD,
∵
 |
| BD |
 |
| BM |
∴∠BDM=∠BAD,
∴∠BDM=∠G,
∴FD=FG.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
 如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数
如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数| 18 |
| A、点O和A之间 |
| B、点A和B之间 |
| C、点B和C之间 |
| D、点C和D之间 |
下列多项式中,属于二次三项式的是( )
| A、2a+b+c |
| B、a2b+ab+ab2 |
| C、2x+1-x2 |
| D、a2-2ab+b2-1 |
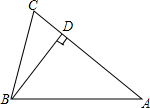 如图,在△ABC中,BD⊥AC于D,sinA=
如图,在△ABC中,BD⊥AC于D,sinA=