题目内容
1.一次作业中,小华作业中,小华做了这样一道,以下是他的解题过程:题目:当m为何值时,关于x的方程x2+(m+2)x+2m-1=0的两根互为相反数?
解:因为:关于x的方程x2+(m+2)x+2m-1=0的两根互为相反数;
所以:$\left\{\begin{array}{l}{{k}^{2}+(m+2)k=2m-1=0(1)}\\{(-k)^{2}+(m+2)(-k)+2m-1=0(2)}\end{array}\right.$
(1)式减(2)式得:2(m+2)k=0
所以:m=-2或k=0;把k=0代入(1)式,得m=$\frac{1}{2}$
所以:m=-2或m=$\frac{1}{2}$
(1)请你把m的值代入原方程;分别求出这两种情况下,关于x的方程的两个根;
(2)判断这两个m是否都正确;如果解题错误,请找出错误原因.
分析 (1)当m=-2时,原方程化为x2-5=0,当m=$\frac{1}{2}$时,原方程化为x2+$\frac{5}{2}$x=0,分别求出方程的根即可;
(2)根据原方程的题意判断即可.
解答 解:(1)当m=-2时,原方程化为x2-5=0,
解得:x1=-$\sqrt{5}$,x2=$\sqrt{5}$,
当m=$\frac{1}{2}$时,原方程化为x2+$\frac{5}{2}$x=0,
解得:x1=0,x2=-$\frac{5}{2}$;
(2)m=$\frac{1}{2}$不正确,
当m为何值时,关于x的方程x2+(m+2)x+2m-1=0的两根互为相反数,解决这类问题,要根据根与系数的关系来解决,
错误的原因是没有按照根与系数的关系来解.
点评 此题考查了一元二次方程根与系数的关系,设一元二次方程ax2+bx+c=0的两个根为x1,x2,当b2-4ac≥0时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.现有3cm,3m,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.在现实生活中,用地砖铺地,用瓷砖贴膜,都要求砖于砖之间严丝合缝、不留空隙、不能重叠,这些工作从数学的角度解释,就叫用多边形覆盖平面(或平面镶嵌),下面不能用于平面镶嵌的图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
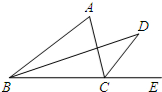 如图,B、C、E三点共线,BD平分∠ABC,CD平分∠ACE,
如图,B、C、E三点共线,BD平分∠ABC,CD平分∠ACE,