题目内容
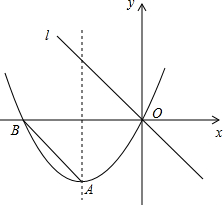 如图,对称轴为x=-3的抛物线y=ax2+2x 与x 轴相交于点B、O.连结AB,把AB所在的直线平移,使它经过原点O,得到直线l(1)①求抛物线的解析式,并求出顶点A 的坐标;
如图,对称轴为x=-3的抛物线y=ax2+2x 与x 轴相交于点B、O.连结AB,把AB所在的直线平移,使它经过原点O,得到直线l(1)①求抛物线的解析式,并求出顶点A 的坐标;②求直线l的函数解析式.
(2)若点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当9<S≤18时,t的取值范围;
(3)在(2)的条件下,当t取最小值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边?若存在,直接写出点Q的坐标;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)根据抛物线的对称轴方程即可确定a的值,由此可得到抛物线的解析式,通过配方可求出顶点A的坐标;
(2)根据A、B的坐标,易求得直线AB的解析式,进而可确定直线l的解析式,即可表示出P点的坐标;由于P点的位置不确定,因此本题要分成两种情况考虑:
①P点位于第四象限,此时t>0,四边形AOPB的面积可由△OAB和△OBP的面积和求得,由此可得到关于S、t的函数关系式,根据S的取值范围即可判断出t的取值范围;
②P点位于第二象限,此时t<0,可分别过A、P作x轴的垂线,设垂足为N、M;那么四边形AOPB的面积即可由梯形APMN与△ABN的面积和再减去△OPM的面积求得,由此可得到关于S、t的函数关系式,可参照①的方法求出t的取值范围;
结合上面两种情况即可得到符合条件的t的取值范围;
(3)根据(2)的结论,可求出t的最大值,由此可得到P点的坐标;若△OPQ为直角三角形且OP为直角边,那么有两种情况需要考虑:①∠QOP=90°,②∠OPQ=90°;可分别过Q、O作直线l的垂线m、n,由于互相垂直的两直线斜率的乘积为-1,根据直线l的解析式以及Q、O的坐标,即可求出直线m、n的解析式,联立抛物线的解析式即可求出Q点的坐标.
(2)根据A、B的坐标,易求得直线AB的解析式,进而可确定直线l的解析式,即可表示出P点的坐标;由于P点的位置不确定,因此本题要分成两种情况考虑:
①P点位于第四象限,此时t>0,四边形AOPB的面积可由△OAB和△OBP的面积和求得,由此可得到关于S、t的函数关系式,根据S的取值范围即可判断出t的取值范围;
②P点位于第二象限,此时t<0,可分别过A、P作x轴的垂线,设垂足为N、M;那么四边形AOPB的面积即可由梯形APMN与△ABN的面积和再减去△OPM的面积求得,由此可得到关于S、t的函数关系式,可参照①的方法求出t的取值范围;
结合上面两种情况即可得到符合条件的t的取值范围;
(3)根据(2)的结论,可求出t的最大值,由此可得到P点的坐标;若△OPQ为直角三角形且OP为直角边,那么有两种情况需要考虑:①∠QOP=90°,②∠OPQ=90°;可分别过Q、O作直线l的垂线m、n,由于互相垂直的两直线斜率的乘积为-1,根据直线l的解析式以及Q、O的坐标,即可求出直线m、n的解析式,联立抛物线的解析式即可求出Q点的坐标.
解答:解:(1)①∵点B与O(0,0)关于x=3对称,
∴点B坐标为(-6,0).
将点B坐标代入y=ax2+2x得:
36a-12=0;
∴a=
.
∴抛物线解析式为y=
x2+2x.
当x=-3时,y=-3
∴顶点A坐标为(-3,-3).
②设直线AB解析式为y=kx+b.
∵A(-3,-3),B(-6,0),
∴
,
解得
,
∴y=-x-6.
∵直线l∥AB且过点O,
∴直线l解析式为y=-x.
(2)∵点P是l上一动点且横坐标为t,
∴点P坐标为(t,-t).
当P在第二象限时(t<0),
S=S△AOB+S△OBP
=
×6×3+
×6×|-t|
=9-3t.
∵0<S≤18,
∴0<9-3t≤18,
∴-3≤t<3.
又∵t<0,
∴-3≤t<0.
当P在第二象限时(t>0),
作PM⊥x轴于M,设对称轴与x轴交点为N,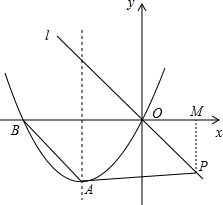
则S=S梯形ANMP+S△ANB-S△PMO
=
(3+t)(3+t)+
×3×3-
t•t=3t+9;
∵0<S≤18,
∴0<3t+9≤18,
∴-3<t≤3;
又∵t>0,
∴0<t<3;
∴t的取值范围是-3≤t<0或0<t<3.
(3)存在,点Q坐标为(3,3)或(6,0)或(3,9).
由(2)知t的最小值为-3,则P(-3,3);
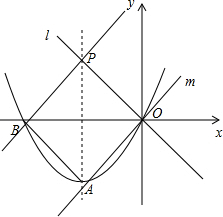 过O、P作直线m、n垂直于直线l;
过O、P作直线m、n垂直于直线l;
∵直线l的解析式为y=-x,
∴直线m的解析式为y=x;
可设直线n的解析式为y=x+h,则有:
-3+h=3,h=6;
∴直线n:y=x+6;
联立直线m与抛物线的解析式有:
,
解得
,
;
∴Q1(-3,-3);
同理可联立直线n与抛物线的解析式,求得Q2(-6,0),Q3(3,9).
∴点B坐标为(-6,0).
将点B坐标代入y=ax2+2x得:
36a-12=0;
∴a=
| 1 |
| 3 |
∴抛物线解析式为y=
| 1 |
| 3 |
当x=-3时,y=-3
∴顶点A坐标为(-3,-3).
②设直线AB解析式为y=kx+b.
∵A(-3,-3),B(-6,0),
∴
|
解得
|
∴y=-x-6.
∵直线l∥AB且过点O,
∴直线l解析式为y=-x.
(2)∵点P是l上一动点且横坐标为t,
∴点P坐标为(t,-t).
当P在第二象限时(t<0),
S=S△AOB+S△OBP
=
| 1 |
| 2 |
| 1 |
| 2 |
=9-3t.
∵0<S≤18,
∴0<9-3t≤18,
∴-3≤t<3.
又∵t<0,
∴-3≤t<0.
当P在第二象限时(t>0),
作PM⊥x轴于M,设对称轴与x轴交点为N,

则S=S梯形ANMP+S△ANB-S△PMO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵0<S≤18,
∴0<3t+9≤18,
∴-3<t≤3;
又∵t>0,
∴0<t<3;
∴t的取值范围是-3≤t<0或0<t<3.
(3)存在,点Q坐标为(3,3)或(6,0)或(3,9).
由(2)知t的最小值为-3,则P(-3,3);
 过O、P作直线m、n垂直于直线l;
过O、P作直线m、n垂直于直线l;∵直线l的解析式为y=-x,
∴直线m的解析式为y=x;
可设直线n的解析式为y=x+h,则有:
-3+h=3,h=6;
∴直线n:y=x+6;
联立直线m与抛物线的解析式有:
|
解得
|
|
∴Q1(-3,-3);
同理可联立直线n与抛物线的解析式,求得Q2(-6,0),Q3(3,9).
点评:此题主要考查了一次函数、二次函数解析式的确定,函数图象交点及图形面积的求法等重要知识点,同时还考查了分类讨论的数学思想,难度较大.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
下列实数中是无理数的是( )
A、
| ||
| B、0 | ||
| C、3.14 | ||
| D、-2 |
 想象一下,将如图的盒子展开成为一个十字型图形,展开后得到的图形是( )
想象一下,将如图的盒子展开成为一个十字型图形,展开后得到的图形是( )A、 |
B、 |
C、 |
D、 |
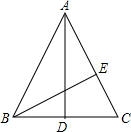 如图,在△ABC中,AB=AC=17,BC=16,AD为中线,BE⊥AC,垂足为E,则AD=
如图,在△ABC中,AB=AC=17,BC=16,AD为中线,BE⊥AC,垂足为E,则AD= 如图,OM平分∠AOB,ON平分∠COD,若∠AOD=70°,∠BOC=10°,则∠MON=
如图,OM平分∠AOB,ON平分∠COD,若∠AOD=70°,∠BOC=10°,则∠MON=