题目内容
某县欲从市场采购60台投影仪配备给县里各中学.经市场调查,符合要求的投影仪只有A、B两种型号,其中A型号投影仪比B型号投影仪每台售价贵2000元,且购买3台A型号投影仪和5台B型号投影仪共需70000元.
(1)求A型号、B型号投影仪每台售价各为多少元?
(2)设该县购买A型号投影仪m(台),购买60台投影仪的总费用为w(元),求w与m的函数表达式;
(3)如果该县购买A型号投影仪的数量不少于B型号投影仪数量的2倍,那么购买这60台投影仪费用最少需要多少元?
(1)求A型号、B型号投影仪每台售价各为多少元?
(2)设该县购买A型号投影仪m(台),购买60台投影仪的总费用为w(元),求w与m的函数表达式;
(3)如果该县购买A型号投影仪的数量不少于B型号投影仪数量的2倍,那么购买这60台投影仪费用最少需要多少元?
考点:一次函数的应用
专题:
分析:(1)设A型号投影仪每台x元,B型号的投影仪每台y元,根据条件建立方程组求出其解即可;
(2)由(1)的结论,根据总费用=两种型号的投影仪费用之和就可以求w与m之间的关系式;
(3)根据题意建立不等式求出m的取值范围,由(2)的解析式就可以求出结论.
(2)由(1)的结论,根据总费用=两种型号的投影仪费用之和就可以求w与m之间的关系式;
(3)根据题意建立不等式求出m的取值范围,由(2)的解析式就可以求出结论.
解答:解:(1)设A型号投影仪每台x元,B型号的投影仪每台y元,由题意,得
,
解得:
.
答:A型号投影仪每台10000元,B型号的投影仪每台8000元;
(2)由题意,得
w=10000m+8000(60-m)=2000m+480000.
答:w与m的函数表达式为w=2000m+480000;
(3)由题意,得
m≥2(60-m),
m≥40.
∵w=2000m+480000,
∴k=2000>0,
∴w随m的增大而增大,
∴m=40时,w最小=560000.
答:购买这60台投影仪费用最少需要560000元.
|
解得:
|
答:A型号投影仪每台10000元,B型号的投影仪每台8000元;
(2)由题意,得
w=10000m+8000(60-m)=2000m+480000.
答:w与m的函数表达式为w=2000m+480000;
(3)由题意,得
m≥2(60-m),
m≥40.
∵w=2000m+480000,
∴k=2000>0,
∴w随m的增大而增大,
∴m=40时,w最小=560000.
答:购买这60台投影仪费用最少需要560000元.
点评:本题考查了列二元一次方程组解实际问题的运用,总价=单价×数量的运用,一次函数的解析式的运用,一次函数的性质的运用,一元一次不等式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法种数共有( )
| A、6种 | B、5种 | C、4种 | D、3种 |
点P(-2,-1)关于y轴对称的点的坐标是( )
| A、(-2,-1) |
| B、(1,-2) |
| C、(2,-1) |
| D、(-1,-2) |
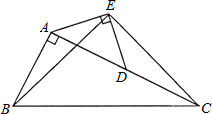 如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
如图,在Rt△ABC中,∠BAC=90°,AB=AD,点D是AC的中点,将一块等腰直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.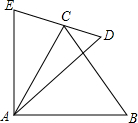 已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证:
已知,如图AE=AC,AD=AB,∠EAC=∠DAB.求证: 某空调室外机形状是一个长方体,其长、宽、高尺寸分别为850mm,320mm,580mm,在朝外一面上有一个圆形的孔,孔的直径为440mm,除这个孔外,外壳均用铁皮包裹.则外壳铁皮的面积(π取3)为
某空调室外机形状是一个长方体,其长、宽、高尺寸分别为850mm,320mm,580mm,在朝外一面上有一个圆形的孔,孔的直径为440mm,除这个孔外,外壳均用铁皮包裹.则外壳铁皮的面积(π取3)为