��Ŀ����
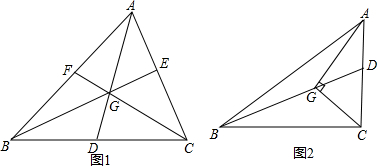
6��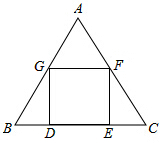 ��ABC��һ��ȱ������εķ���Ƭ�����������һ��������DEFG��ʹ�����ε�һ����DE����BC�ϣ�����F��G�ֱ�����AC��AB�ϣ�
��ABC��һ��ȱ������εķ���Ƭ�����������һ��������DEFG��ʹ�����ε�һ����DE����BC�ϣ�����F��G�ֱ�����AC��AB�ϣ�С�Ϻ�С����������һ���뷨��
��1��С���룺Ҫ����������DEFG��ֻҪ�ܼ���������εı߳��������BD��CE�ij����Ӷ�ȷ��D���E�㣬�ٻ�������DEFG�������ˣ����ABC�ı߳�Ϊ2�������С����������εı߳�������ú����ŵ�ʽ�ӱ�ʾ����Ҫ��
���� ����A��AH��BC��H��FG��K���������εı߳�Ϊx��Ȼ�������AGF�͡�ABC���ƣ��������������ζ�Ӧ�߸ߵıȵ������Ʊ���ʽ���㼴�ɵý⣮
��� 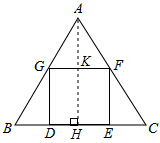 �⣺��ͼ������A��AH��BC��H��FG��K���������εı߳�Ϊx��
�⣺��ͼ������A��AH��BC��H��FG��K���������εı߳�Ϊx��
�ߵȱߡ�ABC�ı߳�Ϊ2��
��AH=2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
�������ζԱ�DE��FG��
���AGF�ס�ABC��
��$\frac{AK}{AH}$=$\frac{GF}{BC}$��
��$\frac{\sqrt{3}-x}{\sqrt{3}}$=$\frac{x}{2}$��
���x=4$\sqrt{3}$-6��
��С�����εı߳�Ϊ4$\sqrt{3}$-6��
���� ���⿼�������������ε�Ӧ�ã��ȱ������ε����ʣ������ε����ʣ���Ҫ���������������ζ�Ӧ�ߵıȵ������Ʊȣ���������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
�����Ŀ
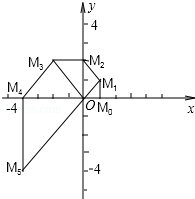 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��M0������Ϊ��1��0�������߶�OM0��ԭ��O��ʱ�뷽����ת45�㣬�ٽ����ӳ���M1��ʹ��M1M0��OM0���õ��߶�OM1���ֽ��߶�OM1��ԭ��O��ʱ�뷽����ת45�㣬�ٽ����ӳ���M2��ʹ��M2M1��OM1���õ��߶�OM2�������ȥ���õ��߶�OM3��OM4��OM5�����������Ϲ��ɣ���ֱ��д��OM2016�ij���Ϊ21008��
��ͼ����ƽ��ֱ������ϵxOy�У���֪��M0������Ϊ��1��0�������߶�OM0��ԭ��O��ʱ�뷽����ת45�㣬�ٽ����ӳ���M1��ʹ��M1M0��OM0���õ��߶�OM1���ֽ��߶�OM1��ԭ��O��ʱ�뷽����ת45�㣬�ٽ����ӳ���M2��ʹ��M2M1��OM1���õ��߶�OM2�������ȥ���õ��߶�OM3��OM4��OM5�����������Ϲ��ɣ���ֱ��д��OM2016�ij���Ϊ21008��
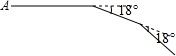 ��ͼ��С����A�����ǰ��10m������ת18�㣬��ǰ��10m��������ת18�㣬��������һֱ����ȥ������һ�λص�������Aʱ��һ������200m��
��ͼ��С����A�����ǰ��10m������ת18�㣬��ǰ��10m��������ת18�㣬��������һֱ����ȥ������һ�λص�������Aʱ��һ������200m��