题目内容
4. 如图,AB是⊙O的直径,点P在BA的延长线上,过点P作⊙O的切线,切点为D,PD的延长线与弦BE的延长线交于点C,连接BD.
如图,AB是⊙O的直径,点P在BA的延长线上,过点P作⊙O的切线,切点为D,PD的延长线与弦BE的延长线交于点C,连接BD.(1)当点D为弧AE的中点时,试判断△PBC的形状,并说明理由;
(2)连接AE,当BC=12,PC=16时,在(1)的条件下,求AE的长.
分析 (1)首先连接OD,由过点P作⊙O的切线,切点为D,可得OD⊥PC,又由点D为弧AE的中点,根据垂径定理即可求得OD⊥AE,AB是⊙O的直径,易证得OD∥BC,即可证得∠C=90°,判定△PBC是直角三角形;
(2)首先过点D作DF⊥PB于点F,由点D为弧AE的中点,可判定BD是∠PBC的角平分线,则可得CD=DF,然后利用三角形的面积,求得CD的长,易证得△POD∽△PBC,可求得OD的长,又由△ABE∽△PBC,求得AE的长.
解答 解:(1)△PBC是直角三角形.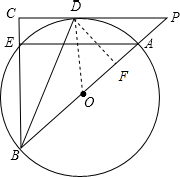 理由:连接OD,
理由:连接OD,
∵PD是⊙O的切线,
∴OD⊥PD,
∵点D为弧AE的中点,
∴OD⊥AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴AE⊥BE,
∴OD∥BE,
∴BC⊥PC,
即△PBC是直角三角形;
(2)过点D作DF⊥PB于点F,
∵点D为弧AE的中点,
∴$\widehat{DE}$=$\widehat{DA}$,
∴∠CBD=∠PBD,
∵BC⊥PC,
∴DC=DF,
设CD=x,则DF=x,
∵BC⊥PC,BC=12,PC=16,
∴PB=$\sqrt{B{C}^{2}+P{C}^{2}}$=20,
∵S△PBC=S△BCD+S△PBD,
∴$\frac{1}{2}$BC•PC=$\frac{1}{2}$BC•CD+$\frac{1}{2}$PB•DF,
即$\frac{1}{2}$×12×16=$\frac{1}{2}$×12x+$\frac{1}{2}$×20x,
解得:x=6,
∴CD=6,
∴PD=PC-CD=10,
∵OD∥BC,
∴△POD∽△PBC,
∴$\frac{PD}{PC}=\frac{OD}{BC}$,
即$\frac{10}{16}=\frac{OD}{12}$,
解得:OD=7.5,
∴AB=2OD=15,
∵∠AEB=∠C=90°,∠ABE=∠PBC,
∴△ABE∽△PBC,
∴$\frac{AE}{PC}=\frac{AB}{PB}$,
即$\frac{AE}{16}=\frac{15}{20}$,
解得:AE=12.
点评 此题考查了切线的性质、垂径定理、圆周角定理以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

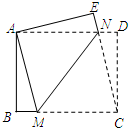 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
| A. | x<-2 | B. | x>-2 | C. | x<14 | D. | x>14 |
| A. | x+5=1 | B. | x-5=1 | C. | x+5=2x-5 | D. | x-5=2x-5 |
 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.