题目内容
 如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4.
如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4.(1)若BC=2
| 3 |
(2)若BC=3,求CD长.
考点:切线的判定
专题:证明题
分析:(1)根据圆周角定理,由AB为⊙O的直径得∠ACB=90°,则根据勾股定理可计算出AC=2,根据含30度的直角三角形三边的关系得到∠ABC=30°,则∠BCO=∠OBC=30°,由于BC=BD,所以∠D=∠BCO=30°,根据三角形外角性质得∠BOD=∠OCB+∠OBC=60°,于是利用三角形内角和定理得到∠OBD=90°,得到OB⊥BD,然后根据切线的判定定理即可得到BD是⊙O的切线;
(2)作BH⊥CD于H,如图,根据等腰三角形的性质得CH=DH,再证明Rt△BHC∽Rt△ACB,利用相似比可计算出CH=
,所以CD=2CH=
.
(2)作BH⊥CD于H,如图,根据等腰三角形的性质得CH=DH,再证明Rt△BHC∽Rt△ACB,利用相似比可计算出CH=
| 9 |
| 4 |
| 9 |
| 2 |
解答:(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,∵AB=4,BC=2
,
∴AC=
=2,
∴∠ABC=30°,
∵OB=OC,
∴∠BCO=∠OBC=30°,
∵BC=BD,
∴∠D=∠BCO=30°,
而∠BOD=∠OCB+∠OBC=60°,
∴∠OBD=90°,
∴OB⊥BD,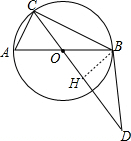
∴BD是⊙O的切线;
(2)解:作BH⊥CD于H,如图,
∵BC=BD,
∴CH=DH,
∵OB=OC,
∴∠BCO=∠OBC,
∴Rt△BHC∽Rt△ACB,
∴
=
,即
=
,
∴CH=
,
∴CD=2CH=
.
∴∠ACB=90°,
在Rt△ACB中,∵AB=4,BC=2
| 3 |
∴AC=
| AB2-BC2 |
∴∠ABC=30°,
∵OB=OC,
∴∠BCO=∠OBC=30°,
∵BC=BD,
∴∠D=∠BCO=30°,
而∠BOD=∠OCB+∠OBC=60°,
∴∠OBD=90°,
∴OB⊥BD,

∴BD是⊙O的切线;
(2)解:作BH⊥CD于H,如图,
∵BC=BD,
∴CH=DH,
∵OB=OC,
∴∠BCO=∠OBC,
∴Rt△BHC∽Rt△ACB,
∴
| CH |
| BC |
| BC |
| AB |
| CH |
| 3 |
| 3 |
| 4 |
∴CH=
| 9 |
| 4 |
∴CD=2CH=
| 9 |
| 2 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.善于使用相似三角形的性质进行几何计算.

练习册系列答案
相关题目
一元二次方程x(x-2)=0的根是( )
| A、0 | B、2 | C、0和2 | D、无解 |
 一个射手连续射靶10次,成绩(环)如图,则该射手射中环数的中位数和众数分别为( )
一个射手连续射靶10次,成绩(环)如图,则该射手射中环数的中位数和众数分别为( )| A、8,9 | B、8,8 |
| C、8.5,8 | D、8.5,9 |
 如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.
如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.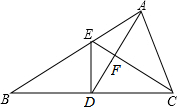 如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,
如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,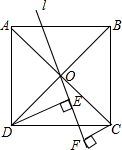 如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明.
如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明. 如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为
如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为 如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为
如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为