题目内容
13.若关于x的方程x2+bx=5的解为x1,x2,则x1x2=-5.分析 用一元二次方程根与系数的关系可直接解答.
解答 解:∵关于x的方程x2+bx=5的解为x1,x2,
∴x1x2=-5,
故答案为:-5.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.下列多项式的乘法中,可以用平方差公式计算的是( )
| A. | (x+1)(1+x) | B. | (-x+y)(-x-y) | C. | (-a+b)(a-b) | D. | (x2-y)(x+y2) |
4.下表是根据方程x2+3x-4=0所列:
则根据表中数据可以判断此方程的一个根是x=1.
| x | 0 | 1 | 2 | 3 | 4 |
| x2+3x-4 | -4 | 0 | 6 | 14 | 24 |
5.在平面直角坐标系中,已知点M(1,-4),若将OM绕原点O逆时针旋转180°得到OM1,则点M1所在的位置是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为( )
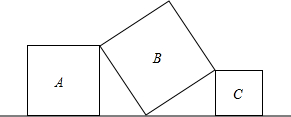

| A. | 25 | B. | 12 | C. | 7 | D. | 5 |
 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.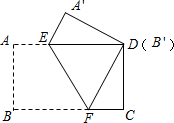 把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求: (1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.
(1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.