题目内容
已知点A(0,2),B(a,0),点C和D在反比例函数y=
的图象上.
(1)若A、B、C、D构成正方形,求a、k的值;
(2)若A、B、C、D构成一个邻边比为2:1的矩形,则k= .
| k |
| x |
(1)若A、B、C、D构成正方形,求a、k的值;
(2)若A、B、C、D构成一个邻边比为2:1的矩形,则k=
考点:反比例函数图象上点的坐标特征
专题:
分析:(1)作CE⊥x轴于E,DF⊥y轴于F,根据题意,△AOB≌△DFA≌△BEC,得出DF=BE=OA=2,AF=CE=OB=a,从而求得C(2+a,a),D(2,2+a),代入y=
,解方程组即可求得a、k的值.
(2))根据题意,△AOB∽△DFA≌△BEC,得出DF=BE=
OA=1,AF=CE=
OB=
a,从而求得C(1+a,
),D(1,2+
),代入y=
,解方程组即可求得a、k的值.
| k |
| x |
(2))根据题意,△AOB∽△DFA≌△BEC,得出DF=BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| k |
| x |
解答: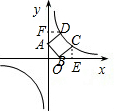 解:(1)如图,作CE⊥x轴于E,DF⊥y轴于F,
解:(1)如图,作CE⊥x轴于E,DF⊥y轴于F,
根据题意,△AOB≌△DFA≌△BEC,
∴DF=BE=OA=2,AF=CE=OB=a,
∴C(2+a,a),D(2,2+a),
∴
,
解得
;
(2)根据题意,△AOB∽△DFA≌△BEC,
∴DF=BE=
OA=1,AF=CE=
OB=
a,
∴C(1+a,
),D(1,2+
),
∴
,
解得k=3.
故答案为3.
 解:(1)如图,作CE⊥x轴于E,DF⊥y轴于F,
解:(1)如图,作CE⊥x轴于E,DF⊥y轴于F,根据题意,△AOB≌△DFA≌△BEC,
∴DF=BE=OA=2,AF=CE=OB=a,
∴C(2+a,a),D(2,2+a),
∴
|
解得
|
(2)根据题意,△AOB∽△DFA≌△BEC,
∴DF=BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴C(1+a,
| a |
| 2 |
| a |
| 2 |
∴
|
解得k=3.
故答案为3.
点评:本题考查了反比例函数图象上的点的坐标特征,三角形全等的性质,三角形相似的性质,数形结合是解本题的关键.

练习册系列答案
相关题目
已知a,b互为相反数,则下列不是相反数的是( )
| A、a3和b3 | ||||
| B、a2和b2 | ||||
| C、-a和-b | ||||
D、
|
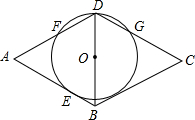 如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点.
如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点. 如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数.
如图,圆心O与△ABC分别截于DE、FG、HM,且DE=FG=HM,若∠A=70°,求∠BOC的度数. 如图,在平行四边形ABCD中,边AB在x轴上,顶点D在y轴上,AB=5,AD=4,点A的坐标为(-1,0),求B、C、D点的坐标.
如图,在平行四边形ABCD中,边AB在x轴上,顶点D在y轴上,AB=5,AD=4,点A的坐标为(-1,0),求B、C、D点的坐标.