题目内容
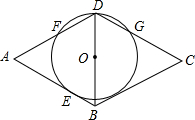 如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点.
如图,已知O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,与AB、CD分别相交于F、G点.(1)求证:BC与⊙O相切;
(2)若∠A=60°,AB=2,求⊙O的半径.
考点:切线的判定,菱形的性质
专题:
分析:(1)利用菱形的性质得出∠ABD=∠CBD,再利用切线的性质得出,∠OEB=90°,进而利用角平分线的性质求出即可;
(2)利用等边三角形的判定以及锐角三角函数关系求出EO的长即可.
(2)利用等边三角形的判定以及锐角三角函数关系求出EO的长即可.
解答: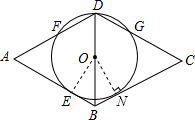 (1)证明:连接EO,作ON⊥BC于点N,
(1)证明:连接EO,作ON⊥BC于点N,
∵O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,
∴∠ABD=∠CBD,∠OEB=90°,
∴OE=ON(角平分线上的点到角的两边距离相等),
∴BC与⊙O相切;
(2)解:∵∠A=60°,AD=AB,
∴△ABD是等边三角形,
∴AB=BD=2,∠ABD=60°,
∴设EO=x,则BO=2-x,
∴sin60°=
=
=
,
解得:x=4
-6,
即⊙O的半径为:4
-6.
 (1)证明:连接EO,作ON⊥BC于点N,
(1)证明:连接EO,作ON⊥BC于点N,∵O是菱形ABCD对角线BD上的一点,以O为圆心,OD为半径的⊙O与AB相切于E点,
∴∠ABD=∠CBD,∠OEB=90°,
∴OE=ON(角平分线上的点到角的两边距离相等),
∴BC与⊙O相切;
(2)解:∵∠A=60°,AD=AB,
∴△ABD是等边三角形,
∴AB=BD=2,∠ABD=60°,
∴设EO=x,则BO=2-x,
∴sin60°=
| EO |
| BO |
| x |
| 2-x |
| ||
| 2 |
解得:x=4
| 3 |
即⊙O的半径为:4
| 3 |
点评:此题主要考查了菱形的性质以及切线的判定以及等边三角形判定等知识,正确利用菱形的性质求出是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若(m+1)xm(m+2)-1+2mx-1=0是关于x的一元二次方程,则m的值是( )
| A、-3 | B、1或-1 |
| C、-3或1 | D、-1 |
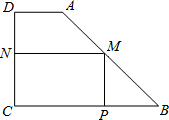 如图所示,有一块形状是直角梯形的铁皮ABCD,它的上底AD=15cm,下底BC=40cm,垂直于底的腰CD=30cm,现要截成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD边上,求矩形MPCN的面积S关于MN的长x的函数关系式.
如图所示,有一块形状是直角梯形的铁皮ABCD,它的上底AD=15cm,下底BC=40cm,垂直于底的腰CD=30cm,现要截成一块矩形铁皮MPCN,使它的顶点M、P、N分别在AB、BC、CD边上,求矩形MPCN的面积S关于MN的长x的函数关系式. 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,
 如图,点C、E、B、F在同一直线上,AB∥DE,A C∥DF,AC=DF,判断CE与FB的数量关系,证明你的结论.
如图,点C、E、B、F在同一直线上,AB∥DE,A C∥DF,AC=DF,判断CE与FB的数量关系,证明你的结论.