题目内容
如图，是由形状大小完全相同的梯形构成的，试观察图形并填表：
| 梯形个数 | 1 | 2 | 3 | 4 | … | 13 |
| 周长 | 3a+b | 4a+2b | 5a+3b | … |
考点：规律型：图形的变化类
专题：
分析：由1个梯形构成的图形周长为3a+b，由2个梯形构成的图形周长为4a+2b，由3个梯形构成的图形周长为5a+3b，所以每增加1个梯形，所构成的图形周长就增加a+b，也可以说，由n个梯形构成的图形周长为（n+2）a+nb，依此求出由4个、13个梯形构成的图形周长．
解答：解：∵由1个梯形构成的图形周长为3a+b，即（1+2）a+b；
由2个梯形构成的图形周长为4a+2b，即（2+2）a+2b；
由3个梯形构成的图形周长为5a+3b，即（3+2）a+3b；
…
∴由n个梯形构成的图形周长为（n+2）a+nb，
∴由4个梯形构成的图形周长为6a+4b，由13个梯形构成的图形周长为15a+13b．
故答案为6a+4b，15a+13b．
由2个梯形构成的图形周长为4a+2b，即（2+2）a+2b；
由3个梯形构成的图形周长为5a+3b，即（3+2）a+3b；
…
∴由n个梯形构成的图形周长为（n+2）a+nb，
∴由4个梯形构成的图形周长为6a+4b，由13个梯形构成的图形周长为15a+13b．
故答案为6a+4b，15a+13b．
点评：本题考查了规律型：图形的变化类，关键是通过归纳与总结，得到由n个梯形构成的图形周长为（n+2）a+nb是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
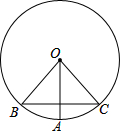如图，在⊙O中，OA⊥BC于G，已知BC=2，OA=2，则∠BOA=