题目内容
5. 如图,在△ABC中,∠ABC=60°,BC=6,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是( )
如图,在△ABC中,∠ABC=60°,BC=6,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是( )| A. | 6 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3 |
分析 作B关于CD的对称点B′,过B′作B′F⊥BC于F交CD于E,则B′F的长度即为BE+EF的最小值,根据直角三角形的性质得到BD=$\frac{1}{2}$CD,根据已知条件得到BB′=BC,推出△CDB≌△BB′F,于是得到B′F=CD=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$.
解答 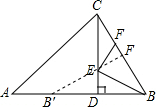 解:作B关于CD的对称点B′,过B′作B′F⊥BC于F交CD于E,
解:作B关于CD的对称点B′,过B′作B′F⊥BC于F交CD于E,
则B′F的长度即为BE+EF的最小值,
∵∠ABC=60°,CD⊥AB,
∴∠BCD=30°,
∴BD=$\frac{1}{2}$CD,
∵BD=$\frac{1}{2}$BB′,
∴BB′=BC,
在△CDB与△B′FB中,
$\left\{\begin{array}{l}{∠CDB=∠B′FB}\\{∠B′BF=∠CBD}\\{CD=BB′}\end{array}\right.$,
∴△CDB≌△BB′F,
∴B′F=CD=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$.
故选C.
点评 本题考查了轴对称-最短路线问题,解题的关键是正确的作出对称点和利用垂直平分线的性质证明BE+EF的最小值为B′F的长度.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.已知二次函数y=x2+bx+c中,其函数y与自变量x之间的部分对应值如下表:
则m的值为-1.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 2 | -1 | -2 | m | 2 | … |
10. 有理数a在数轴上的位置如图所示,下列各数中,可能在0到1之间的是( )
有理数a在数轴上的位置如图所示,下列各数中,可能在0到1之间的是( )
 有理数a在数轴上的位置如图所示,下列各数中,可能在0到1之间的是( )
有理数a在数轴上的位置如图所示,下列各数中,可能在0到1之间的是( )| A. | -a | B. | |a| | C. | |a|-1 | D. | a+1 |
14.(-$\frac{1}{2}$ab3)3•(-$\frac{1}{4}$ab)•(-8a2b2)2等于( )
| A. | 2a8b14 | B. | -2a8b14 | C. | a8b11 | D. | -a8b11 |
 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2).
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2). 如图,已知二次函数y=ax2+bx+c的图象过点A(-1,0)和点C(0,3),对称轴为直线x=1.
如图,已知二次函数y=ax2+bx+c的图象过点A(-1,0)和点C(0,3),对称轴为直线x=1. 如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为(πa2-2a2)(用含a的代数式表示,结果保留π).
如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为(πa2-2a2)(用含a的代数式表示,结果保留π).