题目内容
 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE.且点G在矩形ABCD内部.如果将BG延长交DC于点F.
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE.且点G在矩形ABCD内部.如果将BG延长交DC于点F.(1)则FG
(2)若BC=12cm,CF比DF长1cm,试求线段AB的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设CF=xcm,则BF=x+x-1+x-1=(3x-2)cm,在Rt△BFC中,根据勾股定理求出x,进一步得到线段AB的长.
(2)可设CF=xcm,则BF=x+x-1+x-1=(3x-2)cm,在Rt△BFC中,根据勾股定理求出x,进一步得到线段AB的长.
解答:解:(1)连接EF,
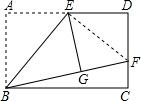 则根据翻折不变性得,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF与Rt△EDF中,
∴Rt△EGF≌Rt△EDF(HL),
∴FG=FD;
(2)设CF=xcm,则BF=x+x-1+x-1=(3x-2)cm,
在Rt△BFC中,BF2=BC2+CF2,
即(3x-2)2=122+x2,
解得x1=-3.5(舍去),x2=5.
AB=x+x-1=2x-1=9cm.
故线段AB的长是9cm.
故答案为:=.
 则根据翻折不变性得,
则根据翻折不变性得,∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF与Rt△EDF中,
|
∴Rt△EGF≌Rt△EDF(HL),
∴FG=FD;
(2)设CF=xcm,则BF=x+x-1+x-1=(3x-2)cm,
在Rt△BFC中,BF2=BC2+CF2,
即(3x-2)2=122+x2,
解得x1=-3.5(舍去),x2=5.
AB=x+x-1=2x-1=9cm.
故线段AB的长是9cm.
故答案为:=.
点评:此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识,难度适中.

练习册系列答案
相关题目
对于不等式组
(a、b是常数),下列说法正确的是( )
|
| A、当a<b时无解 |
| B、当a≥b时无解 |
| C、当a≥b时有解 |
| D、当a=b时有解 |
下列说法:
(1)有且只有一条直线垂直于已知直线;
(2)两条直线相交时,如果对顶角的和是180°,那么这两条直线互相垂直;
(3)过直线a外一点P作PD⊥a,垂足为D,则线段PD是点P到直线a的距离;
(4)在同一平面内,经过一点有且只有一条直线垂直于已知直线.
其中正确的说法有( )
(1)有且只有一条直线垂直于已知直线;
(2)两条直线相交时,如果对顶角的和是180°,那么这两条直线互相垂直;
(3)过直线a外一点P作PD⊥a,垂足为D,则线段PD是点P到直线a的距离;
(4)在同一平面内,经过一点有且只有一条直线垂直于已知直线.
其中正确的说法有( )
| A、(1)(2)(4) |
| B、(3)(4) |
| C、(2)(3) |
| D、(2)(4) |

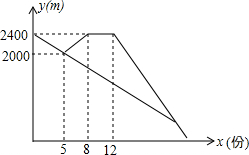 小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题.
小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题. 一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.